The vapor pressure of water at 25 °C is 23.76 torr. If 0.25 g of water is enclosed in a 1.50-L container, will any liquid be present? If so, what mass of liquid?

Verified step by step guidance

1. Calculate the number of moles of water using the formula: \( n = \frac{m}{M} \), where \( m \) is the mass of water (0.25 g) and \( M \) is the molar mass of water (18.02 g/mol).
2. Use the ideal gas law to calculate the pressure exerted by the water vapor if all the water were to vaporize: \( PV = nRT \), where \( P \) is the pressure, \( V \) is the volume (1.50 L), \( n \) is the number of moles calculated in step 1, \( R \) is the ideal gas constant (0.0821 L·atm/mol·K), and \( T \) is the temperature in Kelvin (25 °C = 298 K).
3. Convert the calculated pressure from atm to torr (1 atm = 760 torr) to compare with the given vapor pressure of water at 25 °C (23.76 torr).
4. Compare the calculated vapor pressure with the given vapor pressure of water. If the calculated pressure is greater than 23.76 torr, not all water will vaporize, and some liquid will remain.
5. If liquid remains, calculate the mass of water that remains as liquid by determining the difference between the initial mass and the mass that would vaporize to reach the equilibrium vapor pressure.

Key Concepts

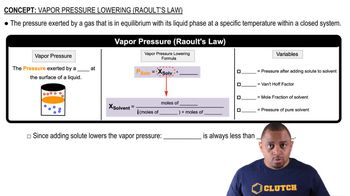
Vapor Pressure

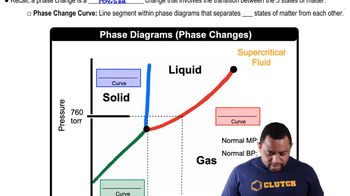
Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid phase at a given temperature. For water at 25 °C, the vapor pressure is 23.76 torr, meaning that at this temperature, water molecules escape into the vapor phase until this pressure is reached. Understanding vapor pressure is crucial for determining whether liquid water will remain in a closed container.

Ideal Gas Law

The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. In this scenario, it can be used to calculate the number of moles of water vapor that can exist in the 1.50-L container at the given vapor pressure. This helps in assessing whether the amount of water vapor exceeds the capacity of the container, indicating if any liquid water will remain.

Phase Equilibrium

Phase equilibrium occurs when the rates of evaporation and condensation of a substance are equal, resulting in a stable amount of liquid and vapor. In this case, if the amount of water vapor produced from the 0.25 g of water exceeds the vapor pressure of 23.76 torr, the system will reach equilibrium with some liquid remaining. Understanding this concept is essential for predicting the presence of liquid water in the container.