If core electrons completely shielded valence electrons from nuclear charge (i.e., if each core electron reduced nuclear charge by 1 unit) and if valence electrons did not shield one another from nuclear charge at all, what would be the effective nuclear charge experienced by the valence electrons of each atom? a. K

Video transcript

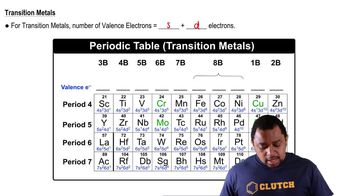
hey everyone in this example, we need to calculate the effective nuclear charge of valence electrons of gallium based on the theoretical conditions where the first is that the core electrons will completely shield electrons from the nuclear charge. And the second being that valence electrons do not shield one another. So what we should first do is recall our formula for effective nuclear charge, which we should recall is represented by this symbol here. And we're going to recall that. That is equal to our atomic number. Z subtracted from our core electrons of our given atom. And so what we're gonna do is analyze gallium. So we would recognize that gallium on the periodic table has a atomic number equal to 31. And so we would say that because it's also at atomic number 31 we would recognize it in Group three A. On the periodic table. And so being in group three a. We want to recall that our group number will correspond to our outer shell of electrons known as our valence electrons. So we would have three valence electrons on our galleon. So our next step is to determine our core electrons on gallium or within galleon. So what we would have is our atomic number minus our valence electrons. And so this is going to be 31. Our atomic number for gallium minus the three valence electrons due to gallium being in group three A. And so this difference gives us a value of 28 core electrons. And so now we can finally calculate our effective nuclear energy of our gallium by taking our atomic number 31 subtracting it from our core electrons in gallium 28 to give us a value equal to positive three or plus three. And so we would say that therefore are effective nuclear charge of gallium is equal to plus three, and this will correspond to choice be in the multiple choice. So everything boxed in blue is our final answer. If you have any questions, please leave them down below and I will see everyone in the next practice video.