Ionization involves completely removing an electron from an atom. How much energy is required to ionize a hydrogen atom in its ground (or lowest energy) state? What wavelength of light contains enough energy in a single photon to ionize a hydrogen atom?
Ch.7 - Quantum-Mechanical Model of the Atom
Chapter 7, Problem 82
Suppose that, in an alternate universe, the possible values of ml are the integer values including 0 ranging from -l -1 to l +1 (instead of simply -l to +l). How many orbitals exist in each sublevel? a. s sublevel b. p sublevel c. d sublevel
 Verified step by step guidance
Verified step by step guidance1
1. In this alternate universe, the magnetic quantum number (ml) ranges from -l -1 to l +1. This means that for each sublevel, there are 2l + 3 possible values of ml, which correspond to the number of orbitals in each sublevel.
2. For the s sublevel, the angular quantum number (l) is 0. So, the number of orbitals is 2*0 + 3 = 3.
3. For the p sublevel, the angular quantum number (l) is 1. So, the number of orbitals is 2*1 + 3 = 5.
4. For the d sublevel, the angular quantum number (l) is 2. So, the number of orbitals is 2*2 + 3 = 7.
5. Therefore, in this alternate universe, there are 3 orbitals in the s sublevel, 5 orbitals in the p sublevel, and 7 orbitals in the d sublevel.

Verified Solution
Video duration:
1mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Quantum Numbers
Quantum numbers are sets of numerical values that describe the unique quantum state of an electron in an atom. The four quantum numbers include the principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (ml), and spin quantum number (ms). Each quantum number provides specific information about the electron's energy level, shape, orientation, and spin, which are essential for understanding electron configurations and orbital shapes.
Recommended video:
Guided course

Principal Quantum Number
Sublevels and Orbitals
Sublevels are divisions of principal energy levels (n) in an atom, characterized by the azimuthal quantum number (l). Each sublevel corresponds to a specific type of orbital: s (l=0), p (l=1), d (l=2), and f (l=3). The number of orbitals within a sublevel is determined by the values of the magnetic quantum number (ml), which indicates the orientation of the orbitals in space. In the standard model, s has 1 orbital, p has 3, and d has 5.
Recommended video:
Guided course

Molecular Orbital Theory
Modified Magnetic Quantum Number
In the given alternate universe scenario, the magnetic quantum number (ml) ranges from -l-1 to l+1, which expands the possible orientations of orbitals. For example, in the s sublevel (l=0), there is still 1 orbital; in the p sublevel (l=1), the range of ml would allow for 3 orbitals; however, in the d sublevel (l=2), the range would now include 5 additional orientations, resulting in a total of 7 orbitals. This modification alters the traditional understanding of orbital availability in each sublevel.
Recommended video:
Guided course
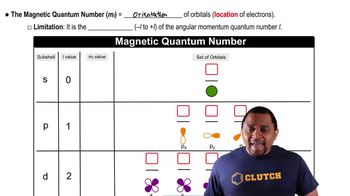
Magnetic Quantum Number
Related Practice
Textbook Question
1801
views
1
comments
Textbook Question
The energy required to ionize sodium is 496 kJ/mol. What minimum frequency of light is required to ionize sodium?
1739
views
1
rank
Textbook Question
Suppose that in an alternate universe, the possible values of l are the integer values from 0 to n (instead of 0 to n - 1). Assuming no other differences between this imaginary universe and ours, how many orbitals would exist in each level? a. n = 1 b. n = 2 c. n = 3
1073
views
Textbook Question
An atomic emission spectrum of hydrogen shows three wavelengths: 1875 nm, 1282 nm, and 1093 nm. Assign these wavelengths to transitions in the hydrogen atom.
3025
views
Textbook Question
An atomic emission spectrum of hydrogen shows three wavelengths: 121.5 nm, 102.6 nm, and 97.23 nm. Assign these wavelengths to transitions in the hydrogen atom.
1868
views
Open Question
The binding energy of electrons in a metal is 193 kJ/mol. What is the threshold frequency of the metal?
