An X-ray photon of wavelength 0.989 nm strikes a surface. The emitted electron has a kinetic energy of 969 eV. What is the binding energy of the electron in kJ/mol? [KE = 1/2 mv2; 1 electron volt (eV) = 1.602×10–19 J]
Suppose that in an alternate universe, the possible values of l are the integer values from 0 to n (instead of 0 to n - 1). Assuming no other differences between this imaginary universe and ours, how many orbitals would exist in each level? a. n = 1 b. n = 2 c. n = 3
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Quantum Numbers

Orbital Types
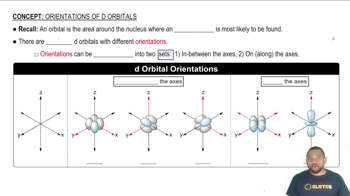
Counting Orbitals

Ionization involves completely removing an electron from an atom. How much energy is required to ionize a hydrogen atom in its ground (or lowest energy) state? What wavelength of light contains enough energy in a single photon to ionize a hydrogen atom?
The energy required to ionize sodium is 496 kJ/mol. What minimum frequency of light is required to ionize sodium?
Suppose that, in an alternate universe, the possible values of ml are the integer values including 0 ranging from -l -1 to l +1 (instead of simply -l to +l). How many orbitals exist in each sublevel? a. s sublevel b. p sublevel c. d sublevel
An atomic emission spectrum of hydrogen shows three wavelengths: 1875 nm, 1282 nm, and 1093 nm. Assign these wavelengths to transitions in the hydrogen atom.
An atomic emission spectrum of hydrogen shows three wavelengths: 121.5 nm, 102.6 nm, and 97.23 nm. Assign these wavelengths to transitions in the hydrogen atom.
