Textbook Question
Many heterogeneous catalysts are deposited on high-surfacearea supports. Why?
625
views
1
rank
 Verified step by step guidance
Verified step by step guidance
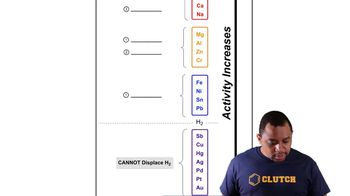


Many heterogeneous catalysts are deposited on high-surfacearea supports. Why?
Suppose that the reaction A¡products is exothermic and has an activation barrier of 75 kJ/mol. Sketch an energy diagram showing the energy of the reaction as a function of the progress of the reaction. Draw a second energy curve showing the effect of a catalyst.
The tabulated data were collected for this reaction at 500 °C: CH3CN(g) → CH3NC( g) a. Determine the order of the reaction and the value of the rate constant at this temperature.
The tabulated data were collected for this reaction at 500 °C: CH3CN(g) → CH3NC( g) b. What is the half-life for this reaction (at the initial concentration)?