Here are the essential concepts you must grasp in order to answer the question correctly.
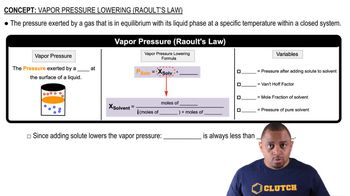
Vapor Pressure
Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid phase at a given temperature. It reflects the tendency of particles to escape from the liquid phase into the vapor phase. Higher vapor pressure indicates a greater volatility of the substance. Understanding vapor pressure is crucial for analyzing mixtures and predicting how components behave under varying conditions.
Recommended video:
Raoult's Law and Vapor Pressure
Raoult's Law
Raoult's Law states that the vapor pressure of a solvent in a solution is directly proportional to the mole fraction of the solvent present. This law is fundamental in understanding how the addition of a solute affects the vapor pressure of a solvent. In this question, Raoult's Law can be applied to determine the contribution of compound X to the overall vapor pressure of the mixture with benzene.
Recommended video:
Raoult's Law and Vapor Pressure
Molar Mass Calculation
Molar mass is the mass of one mole of a substance, typically expressed in grams per mole (g/mol). It is calculated by summing the atomic masses of all atoms in a molecule. In this problem, the molar mass of compound X can be determined by using the vapor pressures of the pure components and the mixture, along with the mass ratio of the components, to find the mole fraction and subsequently the molar mass.
Recommended video:
Molar Mass Calculation Example