Write balanced nuclear equations for the following processes.
(d) Positron emission of 165Ta

Verified step by step guidance

1. Identify the original isotope and its atomic number and mass number. For 165Ta (tantalum), the atomic number (Z) is 73 and the mass number (A) is 165.
2. Understand that positron emission involves the conversion of a proton into a neutron within the nucleus, with the emission of a positron (β⁺) and a neutrino (ν).
3. Write the nuclear equation showing the original nucleus and the emitted particles. The original nucleus is 165Ta.
4. Since a proton is converted into a neutron, the atomic number will decrease by 1, resulting in the formation of a new element with atomic number 72 (hafnium, Hf) and the same mass number 165.
5. The balanced nuclear equation is: ^{165}_{73}Ta \rightarrow ^{165}_{72}Hf + ^{0}_{+1}e + \nu

Key Concepts

Nuclear Reactions

Nuclear reactions involve changes in an atom's nucleus and can result in the transformation of one element into another. These reactions include processes such as alpha decay, beta decay, and positron emission, where particles are emitted from the nucleus, altering the atomic number and mass number of the original atom.

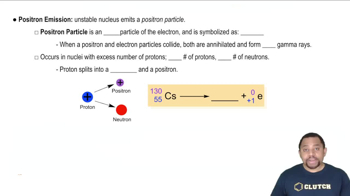
Positron Emission

Positron emission is a type of beta decay where a proton in the nucleus is converted into a neutron, releasing a positron (the antimatter counterpart of an electron) and a neutrino. This process decreases the atomic number by one while keeping the mass number unchanged, resulting in the formation of a new element.

Balancing Nuclear Equations

Balancing nuclear equations requires ensuring that the total number of protons and neutrons is the same on both sides of the equation. This involves accounting for the emitted particles and the resulting nuclide, maintaining conservation of mass and charge throughout the reaction.