The enthalpy of evaporation of water is 40.67 kJ/mol. Sunlight striking Earth's surface supplies 168 W per square meter (1 W = 1 watt = 1 J/s). (a) Assuming that evaporation of water is due only to energy input from the Sun, calculate how many grams of water could be evaporated from a 1.00 square meter patch of ocean over a 12-h day

Question

Accepted Answer

Hey everyone in this example, we're told that light from the sun supplies 168 watts per square meter. We need to calculate the mass of water that can be evaporated from a 2. square meter portion of a pond for a period of eight hours. We're going to assume that the water evaporates due to energy supplied by the sun. And we're given our entropy of vaporization of water equal to 40.67 kg joules per mole. So we want to recall that one watt is equivalent to one Juul per second according to the prompt. Our area is equal to 2.50 square meters. And we're going to make note of our molar mass of water, which from our periodic table we would see has a mass of 18.16 g per mole. And then last from our prompt, we're told at the time period is going to be eight hours. And then we are also told that our energy that is supplied By the sun is equal to 168 watts per square meter. And because we understand that one watt is equal to one jewel per second, we can interpret this as 168 jewels per meter squared times seconds. Now we need to figure out how much energy is supplied during that eight hour period. So we're going to take our eight hours and we're going to convert from hours to minutes by recalling that in one hour. We have 60 minutes. We can now cancel out our units of ours. Now we're going to focus on converting from minutes to seconds. So we would recall that for one minute. We have 60 seconds. We can cancel out minutes. And now we're going to Plug in our energy that is supplied from the sun during that period of time, which according to what we've outlined above. We have these units here, sorry. So we're gonna plug in this, we have 168 units of energy and jewels per meter squared times seconds. So now we're able to cancel our units of seconds. And lastly we want to plug in the area given as 2.50 m squared. So this allows us to also cancel out those square meter units were left with jewels for our unit of energy, which is what we want. And we're going to get that our energy supply during that eight hour period is equal to a value of 1.2096 times 10 to the seventh power jewels. So now going back to the entropy of vaporization of water given as 40. kg joules per mole. We want to convert this into units of joules per mole. So we're going to do so below by recalling that 40.67 kg joules per mole Can be multiplied by the conversion factor where we recalled that we have for one kg jule 10 to the third power jewels. And this here is a multiplication sign. So now we're going to cancel our units of kilo jewels were left with joules per mole. And this is going to give us our entropy of vaporization for water now equal to 40,670 jules per mole. And now we can go ahead and solve for our mass of water by taking our energy supply during the eight hour period, which above we stated is 1.2096 times 10 to the seventh power jewels. We're going to multiply this by our entropy of vaporization of water which we converted to jules per mole. So we have 40,670 jewels for one mole of water. And then we're going to multiply this by our molar mass of water which we stated is equal to For one mole of water 18.16 g. So now we're able to cancel our units of jewels, moles of water. And we're left with grams of water which is going to give us our final results equal to 5.4 times 10 to the positive third power. And we have just units of grams of our water. So this here would be our final answer to complete this example as our mass of water that is evaporated from the area of our pond. So I hope that everything I explained was clear. If you have any questions, just leave them down below and I will see everyone in the next practice video.

Verified Solution

Key Concepts

Enthalpy of Evaporation

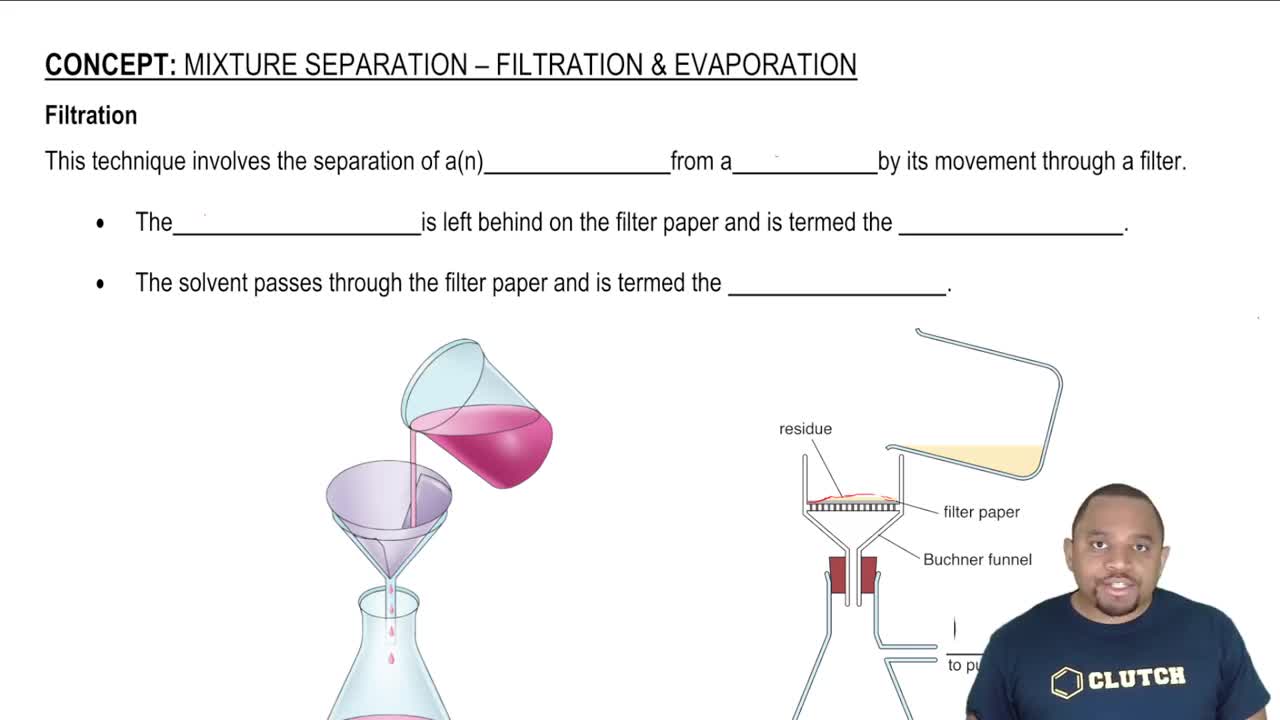
Power and Energy Conversion

Mass-Energy Relationship