Here are the essential concepts you must grasp in order to answer the question correctly.
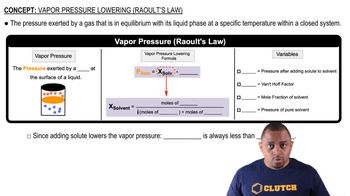
Vapor Pressure
Vapor pressure is the pressure exerted by a vapor in equilibrium with its liquid or solid form at a given temperature. It indicates the tendency of particles to escape from the liquid phase into the gas phase. For water at 30 °C, the vapor pressure is 31.8 torr, meaning that at this temperature, water molecules have a specific tendency to evaporate into the air.
Recommended video:
Raoult's Law and Vapor Pressure
Relative Humidity
Relative humidity is the ratio of the current amount of water vapor in the air to the maximum amount of water vapor the air can hold at that temperature, expressed as a percentage. In this scenario, the air has a relative humidity of 85%, indicating that it contains 85% of the maximum water vapor capacity at 30 °C. This concept is crucial for determining how much water can be removed from the air.
Recommended video:
Ideal Gas Law
The Ideal Gas Law relates the pressure, volume, temperature, and number of moles of a gas through the equation PV = nRT. This law can be applied to calculate the amount of water vapor in the air by converting the vapor pressure into moles and then determining the mass of water that corresponds to those moles. Understanding this relationship is essential for solving the problem of how much water must be removed from the air.
Recommended video: