Ellipses: Standard Form - Online Tutor, Practice Problems & Exam Prep

The ellipse is formed by slicing a cone with a plane at a slight angle, resulting in a shape defined by two axes: the semi-major axis (a) and the semi-minor axis (b). The equations for horizontal and vertical ellipses differ, represented as $x^2/a^2+y^2/b^2=1$ and $x^2/b^2+y^2/a^2=1$, respectively. The vertices and foci are critical points along the major axis, with the foci defined by $c^2=a^2-b^2$. Understanding these concepts is essential for graphing and analyzing ellipses.

Graph Ellipses at Origin

Welcome back, everyone. So up to this point, we've been talking about conic sections. And in the last video, we looked at the circle shape. In this video, we're going to take a look at the ellipse. The ellipse forms when you take a three-dimensional cone and slice it with a two-dimensional plane at a slight angle. Slightly tilt the plane into the cone to give you this ellipse shape, which we're going to talk about in this video. The ellipse is a bit more complicated than the circle because there's more that you need to keep track of when it comes to your graph and equation. But don't sweat it because in this video, we're going to figure out that there are actually some similarities between the circle and the ellipse. And even though it's a bit more complicated, the problem should be pretty straightforward once you know how the equations and graph work. So let's get right into this.

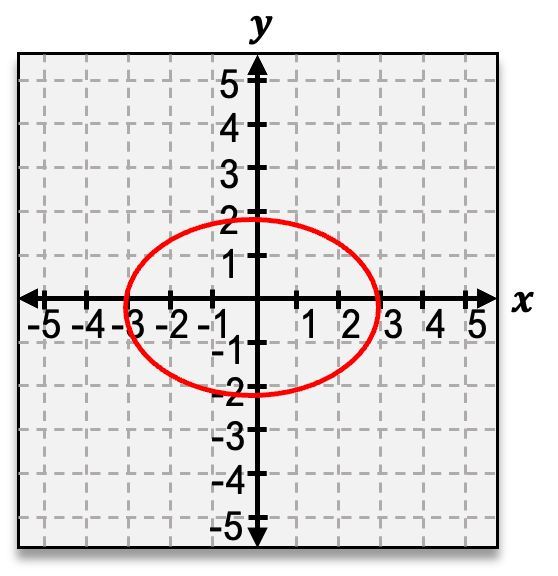
We've already looked at a circle and figured out that the circle depends on its radius. This radius tells us the distance from the center of the circle to any point on it. From this graph here, the circle has a radius of 3 units. That means that any distance you travel to, any point on the circle, is always going to be a distance of 3 from the center. The equation for a circle looks like this:

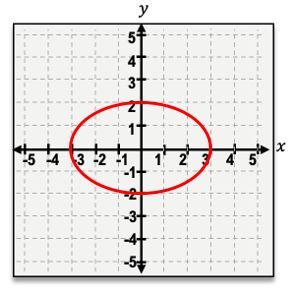
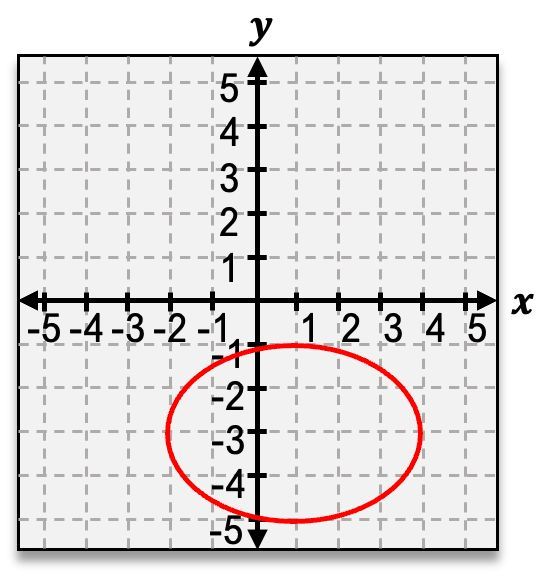
x2 + y2 = r2

Imagine that we take this circle and stretch it horizontally. If we were to stretch this circle, we would end up getting a shape which is a bit different than the circle in that it doesn't have the same symmetry all the way around. Because the distance from the center of the ellipse to this point is not the same as the distance from the center to that point. To define this new shape, there are two distances that we're going to need to keep track of. And this shape is what we call the ellipse because there are going to be 2 distances, which are the semi-major axis and the semi-minor axis that define the shape. The semi-major axis is just going to be the larger of the 2 axes. So if I look at a, I can see that a is 4 units long, and b here is 3 units long. And since a is bigger than b, that means a is going to be the semi-major axis, whereas b is going to be the semi-minor axis.

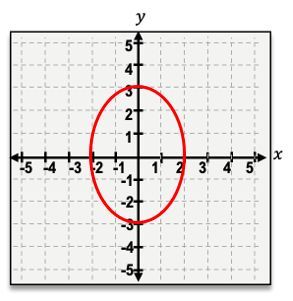
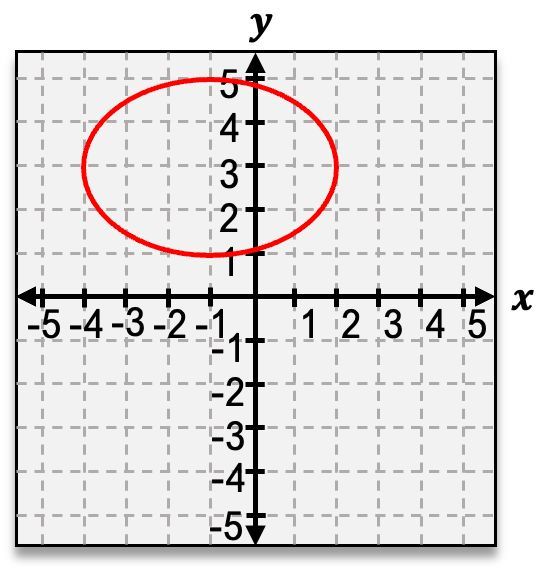
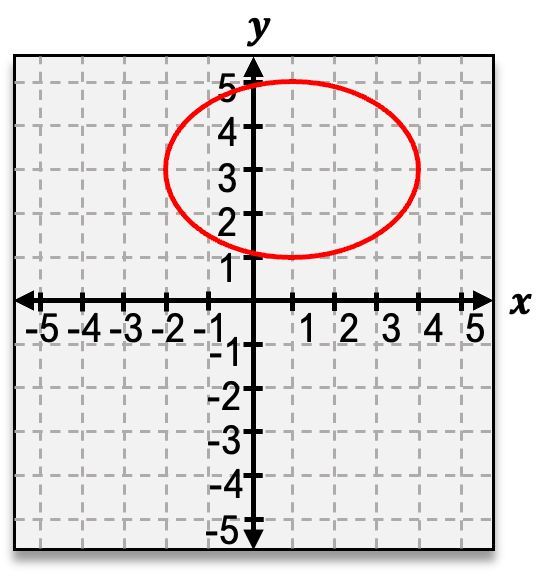
This is the main idea of the horizontal ellipse. But what do you think would happen if we took this same circle and now stretched it vertically instead of horizontally? If we vertically stretch the circle, we would end up getting a vertical ellipse. The way the vertical ellipse works is the major axis, where the ellipse is stretched, is now going to be on the y rather than the x. For our vertical ellipse, a is still 4 units but this time a is up and down rather than left and right. And if we look at our b value, well, we can see that b is still 3 units long, but now b is left and right rather than being up and down like before. So a is still the semi-major axis, and b is still the semi-minor axis, but now it's just the directions that are switched.

The equations for the ellipses are as follows. For the horizontal ellipse, the equation is: x2 a2 + y2 b2 = 1 and for the vertical ellipse, the equation where a2 and b2 are switched to accommodate the stretch on the y axis: x2 b2 + y2 a2 = 1 It's important to know that whenever you see this variable a, it always tells you the longest distance from the center of the ellipse to the outside.

One more thing I want to mention is just kind of a way to remember these equations. If you take the circle equation and rewrite it by dividing r2 by every term, which you can do if you do it to both sides of the equation, you can cancel the r2s, giving you x2r2 plus y2r2 equals 1. Notice how this equation looks similar to the other two equations for the ellipses. The only main difference is this distance is the same. It's the radius because we have symmetry all the way around the circle. Whereas these two equations have 2 different distances, a and b, because we don't have the same symmetry all the way around the shape.

This is the main idea and concepts behind the graphs of ellipses at the origin where the center is right in the middle of the graph. Hope you found this video helpful. Thanks for watching, and let's move on.

Given the equation $\frac{x^2}{4}+\frac{y^2}{9}=1$, sketch a graph of the ellipse.

• A.
• B.
• C.
• D.

Given the ellipse equation $\frac{x^2}{16}+\frac{y^2}{4}=1$, determine the magnitude of the semi-major axis (a) and the semi-minor axis (b).

• A. $a=16$, $b=4$
• B. $a=4$, $b=16$
• C. $a=4$, $b=2$
• D. $a=2$, $b=4$

Foci and Vertices of an Ellipse

Hey, everyone, and welcome back. So in the last video, we were introduced to the concept of an ellipse and how you can graph this shape. In this video, we're going to learn about new elements of the ellipse, specifically the vertices and foci. There are two vertices and two foci for each ellipse. Sometimes, calculating these can be a bit tedious because you will need to know different variables and equations. But don't worry, we're going to find out that the vertices and foci are just various points that you can find along the major axis of the ellipse, depending on how the ellipse is stretched.

Without further ado, let's get right into this. When it comes to the vertices, these are the points on the ellipse that are furthest away from the center. If you have a horizontally stretched ellipse, the vertices are going to be the two points that are furthest from the center along the major axis. Now, you'll also need to know how to find the foci, which are the points that determine the general symmetry of the ellipse. The foci could be right here, for example. They indicate that the sum of any distance from the foci to a single point on the ellipse is always constant. For instance, if we have one distance to a point on the ellipse being 1 and another being 3, then 3 plus 1 equals 4. This tells us that for any point on the ellipse, the sum of the distances from the foci to that point will always sum to 4.

In order to calculate the vertices, you will need the distance for the semi-major axis, denoted as a. This makes sense because if you travel along the semi-major axis in either direction, it will lead you to the vertex points. To find the foci, you will need a distance, c, which relates a and b as follows: c2 = a2 − b2. This will allow you to calculate the distance to the two foci.

Let's take a look at an example where we are asked to find the vertices and foci of an ellipse. Given a2 = 25, we find a = 25 = 5, which is our distance for the semi-major axis. With a calculated, we can determine our vertices. Moving 5 units in each direction from the center will locate our two vertices at 50 and -50. We are also asked to find the foci. Identifying b using b2 = 9, we find b = 9 = 3. From here, we calculate the c value, which reveals the distance to the two foci as follows: If c2 = a2 − b2, then 16 = 4, marking the locations of the foci at 40 and -40.

The arrangement changes if dealing with a vertical ellipse, where the coordinates for the vertices and foci would be on the y-axis. In a horizontal ellipse, as we saw, the vertices and foci are along the x-axis. For a vertical ellipse, you would find the vertices and foci vertically aligned along the y-axis at positions 0, a and 0, −a for vertices, and 0, c and 0, −c for foci. That's the basic idea of finding the vertices and foci of an ellipse. I hope you found this video helpful, and thanks for watching.

Determine the vertices and foci of the following ellipse: $\frac{x^2}{49}+\frac{y^2}{36}=1$.

• A. Vertices: $\left(7,0\right),\left(-7,0\right)$Foci: $\left(6,0\right),\left(-6,0\right)$
• B. Vertices: $\left(6,0\right),\left(-6,0\right)$Foci: $\left(7,0\right),\left(-7,0\right)$
• C. Vertices: $\left(7,0\right),\left(-7,0\right)$Foci: $\left(\sqrt{13},0\right),\left(-\sqrt{13},0\right)$
• D. Vertices: $\left(0,7\right),\left(0,-7\right)$Foci: $\left(0,\sqrt{13}\right),\left(0,-\sqrt{13}\right)$

Determine the vertices and foci of the following ellipse: $\frac{x^2}{9}+\frac{y^2}{16}=1$.

• A. Vertices: $\left(4,0\right),\left(-4,0\right)$Foci: $\left(\sqrt7,0\right),\left(-\sqrt7,0\right)$
• B. Vertices: $\left(0,4\right),\left(0,-4\right)$Foci: $\left(0,\sqrt7\right),\left(0,-\sqrt7\right)$
• C. Vertices: $\left(4,0\right),\left(-4,0\right)$Foci: $\left(3,0\right),\left(-3,0\right)$
• D. Vertices: $\left(0,4\right),\left(0,-4\right)$Foci: $\left(0,3\right),\left(0,-3\right)$

Find the standard form of the equation for an ellipse with the following conditions.

Foci = $\left(-5,0\right),\left(5,0\right)$

Vertices = $\left(-8,0\right),\left(8,0\right)$

• A. $\frac{x^2}{64}+\frac{y^2}{25}=1$
• B. $\frac{x^2}{25}+\frac{y^2}{64}=1$
• C. $\frac{x^2}{8}+\frac{y^2}{5}=1$
• D. $\frac{x^2}{64}+\frac{y^2}{39}=1$

Graph Ellipses NOT at Origin

Hey, everyone, and welcome back. So up to this point, we've been talking about the various shapes and conic sections, and we've specifically been looking at the ellipse in recent videos. Now, all of the ellipses we've dealt with so far have been centered at the origin, where the shape is right in the center of the graph. What would happen if we had our ellipse shifted to some new location, which we'll call (h, k)? How could we deal with these types of ellipses? That's what we're going to be looking at in this video. It turns out the equation and graph do change for this kind of ellipse, but don't sweat it because we're actually going to find that not only is a lot of this stuff straightforward, but it's also pretty familiar to what we've already learned with function transformations. So let's get right into this.

If you have an ellipse that is not at the origin, it is going to be shifted by a certain amount (h, k), where h is the horizontal position and k is the vertical position. We've seen this equation in previous videos, which deals with ellipses at the origin. The equation for an ellipse not at the origin looks like that for this kind of ellipse. And notice that it's actually very similar to the other equation. The only difference is we have this h and k. But just like we get when doing a function transformation where we have a shift, the h and k represent the horizontal and vertical shifts respectively.

To understand this a bit better, let's take a look at an example where we have to graph an ellipse that's not at the origin. In this example, we are given this equation and we're asked to graph the following ellipse. Our first step should be to determine the major and minor axes. To do this, I can look at the equation that we have and see what these are. Recall that the major axis, \(a^2\), is associated with the larger number in the denominator. Since I can see that the larger number is 64, \(a^2 = 64\). This means that \(a\) would be the square root of 64, which is 8. We can also see here that \(b^2\) is going to be associated with the smaller number; that's the minor axis. So \(b^2 = 9\). If \(b^2 = 9\), then \(b\) is going to be the square root of 9, which is 3. So that's our \(a\) and \(b\), which is our major and minor axes.

Our second step asks us to find the orientation of the ellipse, whether it's vertical or horizontal. I can do this by looking for the larger number, which is the major axis squared. I can see that it's 64, and 64 is underneath the \(y\). So because the larger number is underneath the \(y\), that means we're going to be stretched on the \(y\) axis, meaning we're dealing with a vertical ellipse.

The third step asks us to find the center of our ellipse, and to do this, I need to look for \(h\) and \(k\). Based on the equation that we have, \(h\) is going to be what's subtracted from the \(x\), and I can see here that we have \(x-4\). So our \(h\) is going to be 4. And our \(k\) value is going to be associated with what's subtracted from the \(y\) which is 2. So our \(k\) is 2. This means the center of our ellipse is going to be at the horizontal position of 4, and the vertical position of 2.

The fourth step asks us to find the vertices of our ellipse. Since we're dealing with a vertical ellipse, we're going to use these coordinates right here to find the vertices. This tells us we need to add and subtract our major axis from the \(k\) value, which is the vertical position. So, basically, what this is saying is that we need to go up and down rather than left and right to find our vertices. Since I see that our \(a\) value is 8, that means we need to go up 8 units, which would put us right here at \(4,10\). We're going to have a point at \(4, 10\) and then you need to go down 8 units, which would put us down here at \(4, -6\).

The next step asks us to find the \(b\) points. The \(b\) points are associated with vertical oriented ellipses, as we have here. Notice how this asks us to add and subtract from the \(h\) value. That means we need to go left and right. To find the \(b\) points, if I start here at the center, I can take the horizontal position we have \(h\), which is 4, and I can subtract off 3, and that will put us back here because \(4-3\) is positive 1. So that puts us at that point, and then what I need to do is add 3 to 4, and that would put us over here between 6-8 which would be at 7. So the \(b\) points are going to be here at \(1,2\), and over there at \(7,2\).

Our last step asks us to connect these points with a smooth curve. To find the ellipse, what we need to do is take these outside points and connect them with a smooth curve. This will give us the graph of our ellipse.

One more thing that I want to mention is that it's also important to recognize how we could find the foci of an ellipse that's not at the origin. It's actually pretty straightforward because when dealing with a vertical ellipse, you want to use these coordinates for the foci. And when dealing with a horizontal ellipse, you want to use those coordinates for the foci. In this example, we had a vertical ellipse, and all this is saying is that the \(c\) value we talked about calculating in the previous video, you just need to add and subtract that from the vertical position. So if you wanted to find your foci, they're going to be somewhere up here and somewhere down there. That's how you can find the foci of an ellipse. I hope you found this video helpful. Thanks for watching.

Graph the ellipse $\frac{{(x-1)}^2}{9}+\frac{{(y+3)}^2}{4}=1$.

• A.
• B.
• C.
• D.

Determine the vertices and foci of the ellipse $\left(x+1\right)^2+\frac{\left(y-2\right)^2}{4}=1$.

• A. Vertices: $\left(-1,4\right),\left(-1,0\right)$Foci: $\left(-1,2+\sqrt3\right),\left(-1,2-\sqrt3\right)$
• B. Vertices: $\left(-1,4\right),\left(-1,0\right)$Foci: $\left(-2,2\right),\left(0,2\right)$
• C. Vertices: $\left(-2,2\right),\left(0,2\right)$Foci: $\left(1,2+\sqrt3\right),\left(1,2-\sqrt3\right)$
• D. Vertices: $\left(-2,2\right),\left(0,2\right)$Foci: $\left(2+\sqrt3,1\right),\left(2-\sqrt3,1\right)$