Conic sections are fascinating shapes formed by slicing a three-dimensional cone with a two-dimensional plane, and one of the most fundamental shapes is the circle. A circle is defined as the set of all points that are equidistant from a central point, known as the center. This unique property of circles allows us to describe their size and position using specific mathematical equations.
To graph a circle, two key elements are required: the center and the radius. The center is typically denoted as (h, k), where h represents the horizontal position and k represents the vertical position. The radius is the constant distance from the center to any point on the circle. For example, if a circle is centered at the origin (0, 0), the equation can be expressed as:
\[x^2 + y^2 = r^2\]
where r is the radius. If the circle is not centered at the origin, the equation adjusts to account for the new center, taking the form:
\[ (x - h)^2 + (y - k)^2 = r^2 \]
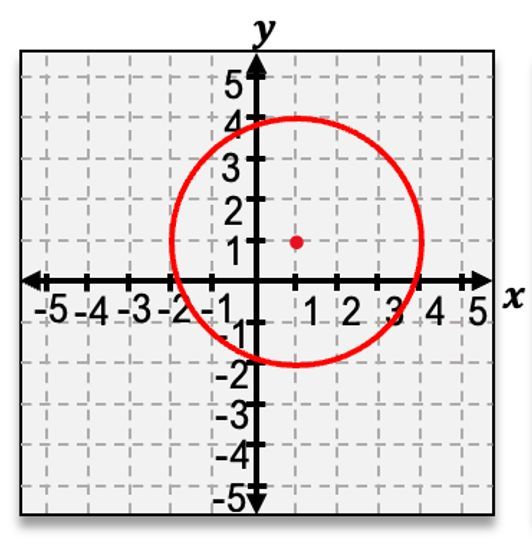
For instance, if a circle has a center at (2, 1) and a radius of 4, the equation would be:
\[ (x - 2)^2 + (y - 1)^2 = 4^2 \]
When given the equation of a circle, one can derive the center and radius to graph it. The center can be identified from the values of h and k, while the radius can be determined by taking the square root of the constant on the right side of the equation. For example, if the equation is:
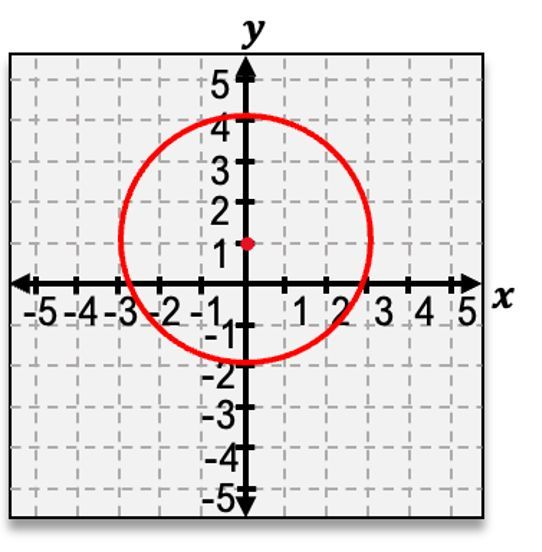
\[ (x - 1)^2 + (y - 2)^2 = 9 \]
the center is (1, 2) and the radius is 3, since \( r^2 = 9 \) implies \( r = \sqrt{9} = 3 \).
To graph the circle, one would plot the center and then mark points at a distance equal to the radius in all four cardinal directions (up, down, left, right) from the center. Connecting these points with a smooth curve results in the visual representation of the circle.
It is important to note that a circle does not represent a function in the mathematical sense, as it fails the vertical line test. This test states that if a vertical line intersects a graph at more than one point, the graph does not represent a function. Since a circle can be intersected by a vertical line at two points, it is classified as a non-function.
Understanding the properties and equations of circles is essential in geometry and serves as a foundation for exploring more complex conic sections.