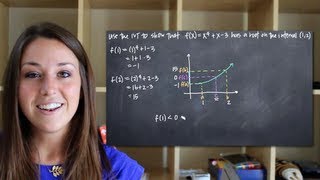4. Polynomial Functions
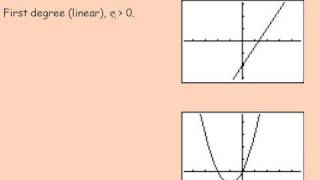
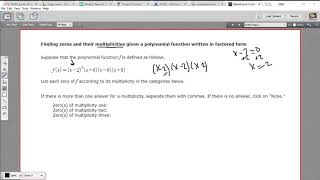
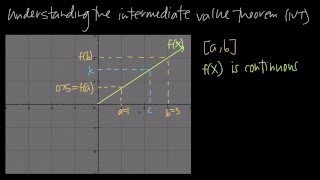
Understanding Polynomial Functions
Learn with other creators
Practice this topic
- Multiple Choice
Determine if the given function is a polynomial function. If so, write in standard form, then state the degree and leading coefficient.
846views13rank - Multiple Choice
Determine if the given function is a polynomial function. If so, write in standard form, then state the degree and leading coefficient.
843views13rank - Multiple Choice
Determine if the given function is a polynomial function. If so, write in standard form, then state the degree and leading coefficient.
1015views2rank - Multiple Choice
Determine the end behavior of the given polynomial function.
1313views2rank - Textbook Question
Determine which functions are polynomial functions. For those that are, identify the degree.
1130views - Textbook Question
Determine which functions are polynomial functions. For those that are, identify the degree.
832views - Textbook Question
Determine which functions are polynomial functions. For those that are, identify the degree.
745views - Textbook Question
Determine which functions are polynomial functions. For those that are, identify the degree.
1021views