8. Conic Sections
Ellipses: Standard Form
8. Conic Sections
Ellipses: Standard Form
Learn with other creators
Practice this topic
- Multiple Choice
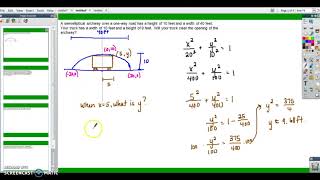
Given the equation , sketch a graph of the ellipse.
792views - Multiple Choice
Given the ellipse equation , determine the magnitude of the semi-major axis (a) and the semi-minor axis (b).
726views1rank - Multiple Choice
Determine the vertices and foci of the following ellipse: .
697views - Multiple Choice
Determine the vertices and foci of the following ellipse: .
601views - Textbook Question
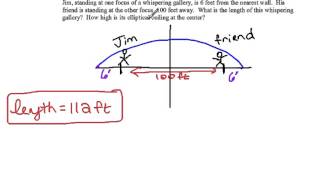
Graph the ellipse and locate the foci. (y^2)/25 + (x^2)/16 = 1
913views - Textbook Question
Find the standard form of the equation of the ellipse satisfying the given conditions. Foci: (-4,0), (4,0); Vertices: (-5,0) (5,0)
2040views1rank1comments - Textbook Question
Find the standard form of the equation of the ellipse satisfying the given conditions. Major axis horizontal with length 12; length of minor axis = 4; center: (-3,5)
1268views1rank - Textbook Question
Graph the ellipse and locate the foci. 9x^2 + 4y^2 - 18x + 8y -23 = 0
1221views