Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Common Functions
Problem 1.3.43b
Textbook Question
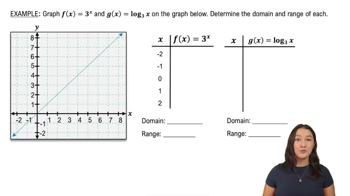
Splitting up curves The unit circle x² + y² = 1 consists of four one-to-one functions, ƒ₁ (x), ƒ₂(x) , ƒ₃(x), and ƒ₄ (x) (see figure)<IMAGE>.
b. Find the inverse of each function and write it as y= ƒ⁻¹ (x)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the unit circle equation x^2 + y^2 = 1, which represents a circle centered at the origin with a radius of 1.
Step 2: Recognize that the unit circle can be divided into four segments, each representing a one-to-one function. These segments correspond to the four quadrants of the circle.
Step 3: Identify the four functions: f₁(x) for the top right quadrant, f₂(x) for the top left quadrant, f₃(x) for the bottom left quadrant, and f₄(x) for the bottom right quadrant.
Step 4: For each function, express y in terms of x. For example, for f₁(x), y = sqrt(1 - x^2) since it represents the top half of the circle where y is positive.
Step 5: Find the inverse of each function by solving for x in terms of y. For instance, for f₁(x), the inverse would be x = sqrt(1 - y^2), and express it as y = f⁻¹(x).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Functions
An inverse function essentially reverses the effect of the original function. If a function ƒ maps an input x to an output y, then its inverse ƒ⁻¹ maps y back to x. For a function to have an inverse, it must be one-to-one, meaning each output is produced by exactly one input. This concept is crucial when finding the inverse of functions derived from the unit circle.
Recommended video:

Inverse Cosine
One-to-One Functions
A one-to-one function is a function where each output is associated with exactly one input, ensuring that no two different inputs produce the same output. This property is essential for determining whether a function has an inverse. In the context of the unit circle, identifying the segments that are one-to-one allows us to find valid inverses for each segment of the curve.
Recommended video:

One-Sided Limits
Unit Circle
The unit circle is a circle with a radius of one centered at the origin of a coordinate plane, defined by the equation x² + y² = 1. It represents all points (x, y) that are one unit away from the origin. Understanding the unit circle is fundamental in trigonometry and calculus, as it provides a geometric representation of sine, cosine, and their inverses, which are often involved in finding the inverses of functions derived from the circle.
Recommended video:
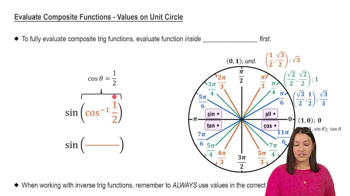
Evaluate Composite Functions - Values on Unit Circle

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice