Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Common Functions
Problem 1.3.43a
Textbook Question
Splitting up curves The unit circle x² + y² = 1 consists of four one-to-one functions, ƒ₁ (x), ƒ₂(x) , ƒ₃(x), and ƒ₄ (x) (see figure) <IMAGE>.
a. Find the domain and a formula for each function.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recognize that the unit circle x^2 + y^2 = 1 can be split into four segments, each representing a one-to-one function. These segments correspond to the four quadrants of the circle.
Step 2: For each quadrant, determine the range of x-values (domain) and the corresponding y-values. The unit circle is symmetric, so consider the signs of x and y in each quadrant.
Step 3: In the first quadrant, both x and y are positive. The function f_1(x) can be expressed as y = sqrt(1 - x^2) with the domain 0 <= x <= 1.
Step 4: In the second quadrant, x is negative and y is positive. The function f_2(x) can be expressed as y = sqrt(1 - x^2) with the domain -1 <= x <= 0.
Step 5: In the third quadrant, both x and y are negative. The function f_3(x) can be expressed as y = -sqrt(1 - x^2) with the domain -1 <= x <= 0.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the unit circle equation x² + y² = 1, the domain must be determined by isolating y in terms of x, which leads to two distinct functions for the upper and lower halves of the circle. Understanding the domain is crucial for identifying valid inputs and ensuring the function behaves correctly within its defined limits.
Recommended video:
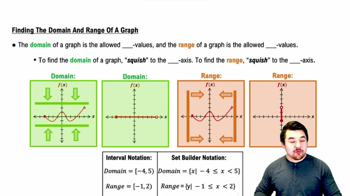
Finding the Domain and Range of a Graph
One-to-One Functions
A one-to-one function is a type of function where each output value is associated with exactly one input value, meaning no two different inputs produce the same output. In the context of the unit circle, splitting it into four one-to-one functions allows us to express the circle in a way that each function can be inverted. This property is essential for solving problems that require finding inverse functions or analyzing the behavior of the functions over their respective domains.
Recommended video:

One-Sided Limits
Implicit vs. Explicit Functions
Implicit functions are defined by an equation involving both variables, such as x² + y² = 1, while explicit functions express one variable directly in terms of another, like y = f(x). To find the formulas for the functions ƒ₁(x), ƒ₂(x), ƒ₃(x), and ƒ₄(x) from the unit circle, one must manipulate the implicit equation to derive explicit forms for y. This distinction is vital for understanding how to work with different types of functions in calculus.
Recommended video:

Finding The Implicit Derivative

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice