Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
5. Graphical Applications of Derivatives
Concavity
Problem 4.R.2e
Textbook Question
Locating extrema Consider the graph of a function ƒ on the interval [-3, 3]. <IMAGE>
e. On what intervals (approximately) is f concave up?
 Verified step by step guidance
Verified step by step guidance1
To determine where the function f is concave up, we need to analyze the second derivative, f''(x). A function is concave up on intervals where its second derivative is positive.
First, find the first derivative f'(x) of the function f. This will help us understand the slope of the tangent line at any point on the graph.
Next, find the second derivative f''(x) by differentiating f'(x). This will give us information about the curvature of the graph.
Examine the sign of f''(x) over the interval [-3, 3]. Identify the subintervals where f''(x) > 0, as these are the intervals where the function is concave up.
If the graph of f is provided, visually inspect the graph to confirm the intervals where the curvature is upwards, which corresponds to f''(x) being positive.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
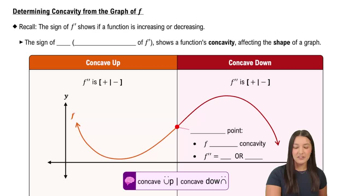
Concavity
Concavity refers to the direction in which a function curves. A function is concave up on an interval if its graph opens upwards, resembling a cup. This occurs when the second derivative of the function is positive, indicating that the slope of the tangent line is increasing.
Recommended video:

Determining Concavity Given a Function
Second Derivative Test
The second derivative test is a method used to determine the concavity of a function. If the second derivative, denoted as f''(x), is greater than zero on an interval, the function is concave up on that interval. Conversely, if f''(x) is less than zero, the function is concave down.
Recommended video:

The Second Derivative Test: Finding Local Extrema
Intervals of Concavity
Intervals of concavity are specific ranges on the x-axis where a function maintains a consistent concavity. To find these intervals, one typically analyzes the sign of the second derivative across the domain of the function, identifying where it remains positive or negative to determine where the function is concave up or down.
Recommended video:

Determining Concavity Given a Function

 6:38m
6:38mWatch next
Master Determining Concavity from the Graph of f with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice