Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
5. Graphical Applications of Derivatives
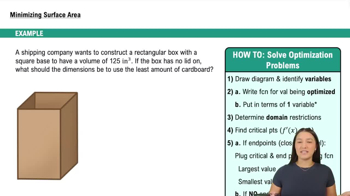
Applied Optimization
Problem 4.8.37a
Textbook Question
{Use of Tech} A damped oscillator The displacement of an object as it bounces vertically up and down on a spring is given by y(t) = 2.5e⁻ᵗ cos 2t, where the initial displacement is y(0) = 2.5 and y = 0 corresponds to the rest position (see figure). <IMAGE>
a. Find the time at which the object first passes the rest position, y = 0.
 Verified step by step guidance
Verified step by step guidance1
Identify the function representing the displacement: y(t) = 2.5e^(-t) * cos(2t).
Set the displacement function equal to zero to find when the object first passes the rest position: 2.5e^(-t) * cos(2t) = 0.
Since 2.5e^(-t) is never zero for any real value of t, focus on solving cos(2t) = 0.
Recall that cos(θ) = 0 at odd multiples of π/2, i.e., θ = (2n+1)π/2 for n being an integer.
Set 2t = (2n+1)π/2 and solve for t to find the first positive time when the object passes the rest position. Start with n = 0 to find the smallest positive t.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Damped Oscillator
A damped oscillator is a system in which the amplitude of oscillation decreases over time due to energy loss, often modeled by an exponential decay function. In the given equation, the term '2.5e⁻ᵗ' represents this damping effect, indicating that the displacement diminishes as time progresses.
Recommended video:

Cases Where Limits Do Not Exist
Trigonometric Functions
The cosine function, represented as 'cos 2t' in the equation, is a periodic function that describes oscillatory motion. It oscillates between -1 and 1, and its argument '2t' indicates the frequency of oscillation, which affects how quickly the object moves up and down.
Recommended video:

Introduction to Trigonometric Functions
Finding Roots of Equations
To find when the object first passes the rest position (y = 0), we need to solve the equation '2.5e⁻ᵗ cos 2t = 0'. This involves determining the values of 't' for which the cosine function equals zero, as the exponential term is never zero. The roots of the cosine function occur at specific intervals, which can be calculated to find the desired time.
Recommended video:
Solving Logarithmic Equations

 1:13m
1:13mWatch next
Master Intro to Applied Optimization: Maximizing Area with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice