How do spermatogenesis and oogenesis in humans differ with respect to numbers of cells produced, gamete size, and timing of the second meiotic division?

The BMI z-score is a relative measure of body mass index (BMI) that takes into account age. Higher values represent heavier individuals for a given height. The table here shows the BMI z-score of pre- and post-pubertal girls at three ages.

Which of the following conclusions can you draw from the data?
a. At a given age, there are more girls with low BMI z-scores than with high BMI z-scores.
b. At a given age, girls with high BMI z-scores are more likely to have begun puberty than girls with low BMI z-scores.
c. Girls 11, 12, and 13 years of age are equally likely to have begun puberty.
d. There is no relationship between BMI z-score and age of beginning puberty.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
BMI z-score
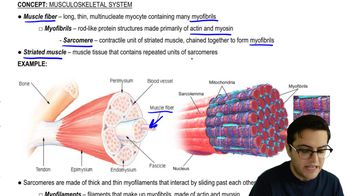
Puberty and its effects on BMI
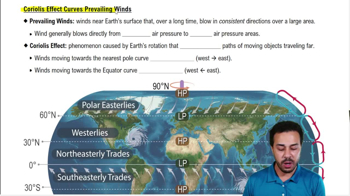
Interpreting data from tables
Give examples of negative and positive feedback in hormonal control of the human menstrual cycle. Why can a high estradiol level be considered a 'readiness' signal from a follicle?
Propose an experiment to test the hypothesis that cells from only one region of a frog blastula form the ectoderm. What results from this experiment would support this hypothesis?
<Image>
In the 1960s, the U.S. Food and Drug Administration approved a contraceptive that allowed women to plan desired pregnancies and prevent unwanted pregnancies. Oral hormonal contraception ('the pill') uses synthetic hormones similar in structure to progesterone and/or estradiol. What is the pill's mechanism of action?
Which of the following is the most effective form of contraception?
a. Condom
b. Diaphragm
c. Withdrawal
d. The pill
<Image>
In the 1960s, the U.S. Food and Drug Administration approved a contraceptive that allowed women to plan desired pregnancies and prevent unwanted pregnancies. Oral hormonal contraception ('the pill') uses synthetic hormones similar in structure to progesterone and/or estradiol. What is the pill's mechanism of action?
Use your knowledge of the hormonal regulation of reproduction to predict the effect of a daily synthetic progesterone pill on (a) pituitary secretion of LH and FSH, and (b) ovarian secretion of estradiol and progesterone.
<Image>
In the 1960s, the U.S. Food and Drug Administration approved a contraceptive that allowed women to plan desired pregnancies and prevent unwanted pregnancies. Oral hormonal contraception ('the pill') uses synthetic hormones similar in structure to progesterone and/or estradiol. What is the pill's mechanism of action?
Scientists confirmed the pill's mechanism of action by measuring plasma hormone levels in women before and after they went on the pill (* means P<0.05, ** means P<0.01, and *** means P<0.001). Do the data shown here support the hypothesis that the pill affects hormonal signaling?
