Textbook Question
Find the area of each triangle ABC.
B = 124.5°, a = 30.4 cm, c = 28.4 cm
172
views
 Verified step by step guidance
Verified step by step guidance

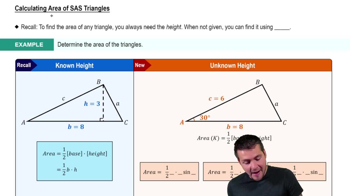

Find the area of each triangle ABC.
B = 124.5°, a = 30.4 cm, c = 28.4 cm
A plane flies 650 mph on a bearing of 175.3°. A 25-mph wind, from a direction of 266.6°, blows against the plane. Find the resulting bearing of the plane.
Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈2, 1〉, 〈-3, 1〉
A pilot is flying at 168 mph. She wants her flight path to be on a bearing of 57° 40′. A wind is blowing from the south at 27.1 mph. Find the bearing she should fly, and find the plane's ground speed.
Find the angle between each pair of vectors. Round to two decimal places as necessary.
〈4, 0〉, 〈2, 2〉
Find the area of each triangle ABC.
A = 59.80°, b = 15.00 cm, C = 53.10°