A plane has an airspeed of 520 mph. The pilot wishes to fly on a bearing of 310°. A wind of 37 mph is blowing from a bearing of 212°. In what direction should the pilot fly, and what will be her ground speed?
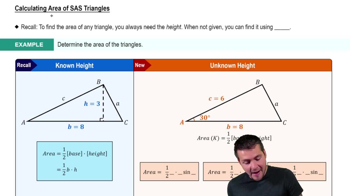
Find the area of each triangle ABC.
A = 42.5°, b = 13.6 m, c = 10.1 m
 Verified step by step guidance
Verified step by step guidance
Verified Solution
Key Concepts
Law of Sines

Area of a Triangle
Angle Measurement in Degrees

CONCEPT PREVIEW Refer to vectors a through h below. Make a copy or a sketch of each vector, and then draw a sketch to represent each of the following. For example, find a + e by placing a and e so that their initial points coincide. Then use the parallelogram rule to find the resultant, as shown in the figure on the right.
<IMAGE>
-b
Determine the number of triangles ABC possible with the given parts.
a = 50, b = 26, A = 95°
Solve each problem. See Examples 5 and 6.
Bearing and Ground Speed of a Plane An airline route from San Francisco to Honolulu is on a bearing of 233.0°. A jet flying at 450 mph on that bearing encounters a wind blowing at 39.0 mph from a direction of 114.0°. Find the resulting bearing and ground speed of the plane.
Find the force required to keep a 75-lb sled from sliding down an incline that makes an angle of 27° with the horizontal. (Assume there is no friction.)
Find the dot product for each pair of vectors.
4i, 5i - 9j
