Here are the essential concepts you must grasp in order to answer the question correctly.
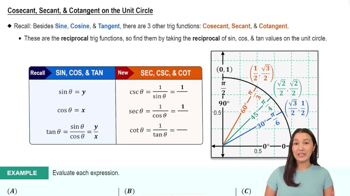
Reciprocal Functions
Reciprocal functions are derived from basic trigonometric functions by taking the reciprocal of their values. For example, the cosecant function is the reciprocal of the sine function, defined as csc(x) = 1/sin(x). Understanding how to transform the graph of a function into its reciprocal is essential for analyzing the behavior of cosecant and secant functions.
Recommended video:
Secant, Cosecant, & Cotangent on the Unit Circle
Graphing Trigonometric Functions
Graphing trigonometric functions involves plotting the values of sine, cosine, and their reciprocals over a specified interval. Key features to consider include the amplitude, period, and asymptotes. Recognizing how the graph of a function changes when moving to its reciprocal is crucial for accurately sketching cosecant and secant graphs.
Recommended video:
Introduction to Trigonometric Functions
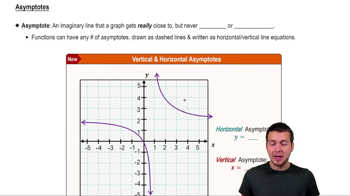
Asymptotes in Trigonometric Functions
Asymptotes are lines that a graph approaches but never touches. For reciprocal trigonometric functions like cosecant and secant, vertical asymptotes occur where the original sine or cosine function equals zero, as these points lead to undefined values in the reciprocal. Identifying these asymptotes is vital for understanding the overall shape and behavior of the reciprocal function's graph.
Recommended video:
 Blitzer 3rd Edition
Blitzer 3rd Edition Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions
Ch. 2 - Graphs of the Trigonometric Functions; Inverse Trigonometric Functions Problem 27
Problem 27 Verified step by step guidance
Verified step by step guidance