Understanding how to plot complex numbers on a graph is essential for visualizing their properties. Complex numbers are expressed in the form x + yi, where x represents the real part and y represents the imaginary part. To plot these numbers, we utilize a complex plane, which consists of a real axis (horizontal) and an imaginary axis (vertical).
When plotting a complex number, the real part indicates the position along the real axis, while the imaginary part indicates the position along the imaginary axis. For example, to plot the complex number 3 + 2i, you would move 3 units to the right on the real axis and 2 units up on the imaginary axis, placing the point at the intersection of these movements.
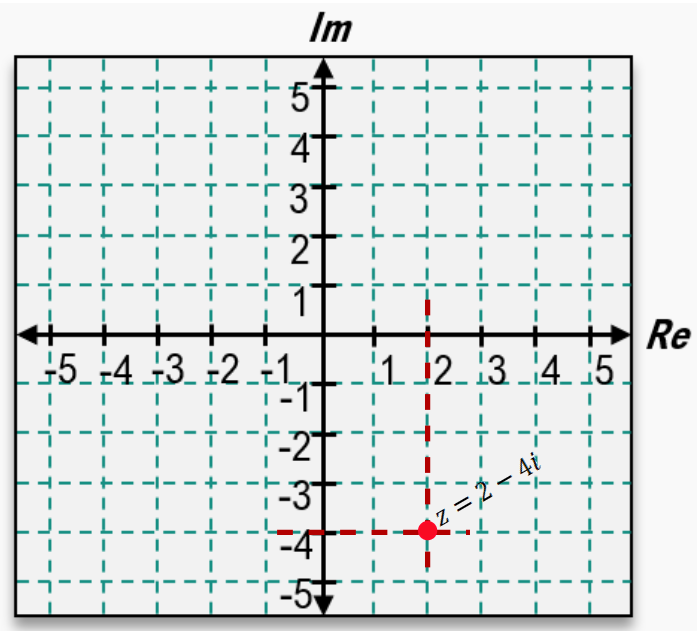
In another example, for the complex number 2 - 4i, the real part is 2, so you move 2 units to the right. The imaginary part is -4, indicating a movement of 4 units down. Thus, the point is plotted accordingly. If you encounter a complex number like 3i, it can be rewritten as 0 + 3i, showing that the real part is 0 and the imaginary part is 3. This means you stay at the origin on the real axis and move 3 units up on the imaginary axis.
In summary, plotting complex numbers involves identifying the real and imaginary components and translating them into movements on the complex plane. This method is straightforward and mirrors the process of plotting points on a standard x-y graph, making it an accessible concept for students to grasp.