4. Graphing Trigonometric Functions

Graphs of Tangent and Cotangent Functions

4. Graphing Trigonometric Functions

Graphs of Tangent and Cotangent Functions: Videos & Practice Problems

Topic summary

The tangent function graph is derived from the identity $ \tan(x) = \frac{\sin(x)}{\cos(x)} $. It features asymptotes at odd multiples of $ \frac{\pi}{2} $ and has a period of $ \frac{\pi}{b} $. The cotangent graph, being the reciprocal of tangent, has asymptotes at integer multiples of $ \pi $ and also shares a period of $ \frac{\pi}{b} $. Understanding these relationships aids in sketching and analyzing their behaviors effectively.

concept

Introduction to Tangent Graph

Video duration:

Introduction to Tangent Graph Video Summary

In exploring the graph of the tangent function, it's essential to understand its relationship with sine and cosine. The tangent of an angle can be expressed as the ratio of sine to cosine, represented mathematically as:

\[ \tan(x) = \frac{\sin(x)}{\cos(x)} \]

Starting from the origin (0,0), we can evaluate the tangent function at key points. At $x = 0$, the tangent value is:

\[ \tan(0) = \frac{\sin(0)}{\cos(0)} = \frac{0}{1} = 0 \]

Moving to $x = \frac{\pi}{4}$, we find:

\[ \tan\left(\frac{\pi}{4}\right) = \frac{\sin\left(\frac{\pi}{4}\right)}{\cos\left(\frac{\pi}{4}\right)} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \]

Conversely, at $x = -\frac{\pi}{4}$, the tangent value is:

\[ \tan\left(-\frac{\pi}{4}\right) = \frac{\sin\left(-\frac{\pi}{4}\right)}{\cos\left(-\frac{\pi}{4}\right)} = \frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1 \]

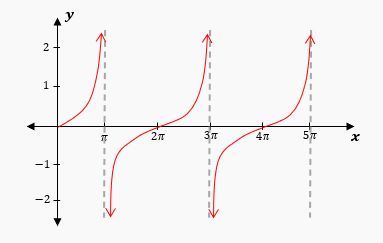
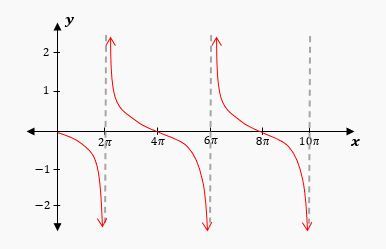
At $x = \frac{\pi}{2}$ and $x = -\frac{\pi}{2}$, the tangent function becomes undefined due to division by zero, leading to vertical asymptotes at these points. The asymptotes for the tangent function occur at odd multiples of $\frac{\pi}{2}$, specifically at:

\[ x = \frac{\pi}{2} + n\pi \quad (n \in \mathbb{Z}) \]

This results in asymptotes at $x = -\frac{3\pi}{2}, -\frac{\pi}{2}, \frac{\pi}{2}, \frac{3\pi}{2}$, indicating that the function approaches infinity at these points. The graph of the tangent function exhibits a repeating pattern every $\pi$ units, distinguishing it from the secant function, which has a period of $2\pi$.

The period of the tangent function can be calculated using the formula:

\[ \text{Period} = \frac{\pi}{b} \]

where $b$ is the coefficient of $x$ in the function. For example, in the function $y = \tan\left(\frac{\pi}{2}x\right)$, the period is:

\[ \text{Period} = \frac{\pi}{\frac{\pi}{2}} = 2 \]

This means the tangent function will repeat its pattern every 2 units along the x-axis. To graph this function, one would plot the asymptotes at $x = -1$ and $x = 1$, and then sketch the curve that rises from the left asymptote to the right asymptote, repeating this pattern every 2 units.

Understanding these properties of the tangent function allows for effective graphing and analysis, reinforcing the connections between trigonometric functions and their graphical representations.

Problem

Below is a graph of the function $y=\tan\left(bx\right)$ . Determine the value of b.

$b=\frac14$

$b=\pi$

$b=2$

$b=\frac12$

example

Example 1

Video duration:

Example 1 Video Summary

To graph the function $ y = \frac{1}{2} \tan\left(x - \frac{\pi}{2}\right) $, we start by analyzing the basic function $ y = \frac{1}{2} \tan(x) $. The tangent function has vertical asymptotes at odd multiples of $ \frac{\pi}{2} $, specifically at $ x = -\frac{\pi}{2} $ and $ x = \frac{\pi}{2} $. The graph of the tangent function typically passes through the origin and has points at $ \left(\frac{\pi}{4}, 1\right) $ and $ \left(-\frac{\pi}{4}, -1\right) $. However, since we have a coefficient of $ \frac{1}{2} $, the amplitude of the graph is reduced, resulting in points at $ \left(\frac{\pi}{4}, \frac{1}{2}\right) $ and $ \left(-\frac{\pi}{4}, -\frac{1}{2}\right) $.

Next, we incorporate the horizontal shift caused by the term $ -\frac{\pi}{2} $. The general form for horizontal shifts in functions is determined by the expression $ h $ in $ (x - h) $. Here, $ h = \frac{\pi}{2} $, indicating a shift to the right. The ratio $ \frac{h}{b} $ helps us understand the shift, where $ b $ is the coefficient of $ x $ (which is 1 in this case). Thus, the shift is $ \frac{\pi}{2} $ units to the right.

To visualize this shift, we take the asymptotes and points from the original graph of $ y = \frac{1}{2} \tan(x) $ and move them $ \frac{\pi}{2} $ units to the right. The asymptote at $ x = -\frac{\pi}{2} $ shifts to $ x = 0 $, and the asymptote at $ x = \frac{\pi}{2} $ shifts to $ x = \pi $. Consequently, the graph will also have an asymptote at $ x = -\pi $ due to the periodic nature of the tangent function, which repeats every $ \pi $ units.

As a result, the final graph of $ y = \frac{1}{2} \tan\left(x - \frac{\pi}{2}\right) $ will exhibit the same shape as the original tangent graph but will be compressed vertically and shifted horizontally to the right by $ \frac{\pi}{2} $ units. The periodicity and asymptotic behavior remain consistent, leading to a complete representation of the function across its defined intervals.

concept

Introduction to Cotangent Graph

Video duration:

Introduction to Cotangent Graph Video Summary

Understanding the cotangent graph is essential for mastering trigonometric functions, especially since it is closely related to the tangent graph. The cotangent function, defined as the reciprocal of the tangent function, can be graphed by identifying its asymptotes and the behavior of its curves.

To begin, recall that the cotangent function is expressed as:

\[ \cot(x) = \frac{1}{\tan(x)} \]

This relationship indicates that wherever the tangent function equals zero, the cotangent function will have vertical asymptotes. For the tangent graph, these points occur at odd multiples of $\frac{\pi}{2}$, specifically at $-\frac{3\pi}{2}$, $-\frac{\pi}{2}$, $\frac{\pi}{2}$, and $\frac{3\pi}{2}$. Consequently, the cotangent graph will have asymptotes at integer multiples of $\pi$, such as $-\pi$, $0$, and $\pi$.

The cotangent graph exhibits a repeating pattern, similar to the tangent graph, with a period of $\pi$. The period of a trigonometric function can be calculated using the formula:

\[ \text{Period} = \frac{\pi}{b} \]

In this case, if $b = 1$, the period simplifies to $1$, indicating that the cotangent function will repeat every unit interval.

When sketching the cotangent graph, the curves will descend from the top left to the bottom right between the asymptotes. For example, between the asymptotes at $0$ and $\pi$, the graph will start from positive infinity and approach zero at $\frac{\pi}{2}$, then continue to negative infinity as it approaches $\pi$. This behavior is mirrored in each subsequent interval.

In summary, the cotangent graph is characterized by its vertical asymptotes at integer multiples of $\pi$, a period of $\pi$, and curves that descend from left to right. Recognizing these features allows for a straightforward sketching process, reinforcing the connection between cotangent and tangent functions.

Problem

Below is a graph of the function $y=\cot\left(bx+\frac{\pi}{2}\right)$ . Determine the value of b.

$b=\frac14$

$b=1$

$b=2$

$b=\frac12$

example

Example 1

Video duration:

Example 1 Video Summary

To graph the function $ y = -2 \cot\left(\frac{1}{4}x\right) $, we need to analyze several components that affect its shape and behavior. The negative sign indicates that the graph will be reflected over the x-axis, while the coefficient of 2 will vertically stretch the graph, altering its amplitude. Additionally, the factor of $ \frac{1}{4} $ inside the cotangent function will affect the period of the graph.

Starting with the basic cotangent function, the period is determined by the formula $ \frac{\pi}{b} $, where $ b $ is the coefficient of $ x $. In this case, since $ b = \frac{1}{4} $, the period becomes:

\[ \text{Period} = \frac{\pi}{\frac{1}{4}} = 4\pi \]

This means the cotangent function will repeat every $ 4\pi $ units. The asymptotes of the cotangent function occur at $ x = 0 $, $ x = 4\pi $, and $ x = 8\pi $. The cotangent graph typically approaches infinity as it nears the asymptotes, decreasing from the left and increasing from the right, with zeros located halfway between the asymptotes.

For the cotangent function $ y = \cot\left(\frac{1}{4}x\right) $, the zeros occur at $ x = \pi $ and $ x = 3\pi $, where the output is 0. The typical outputs at these points are 1 and -1, respectively. However, since we are considering $ y = -2 \cot\left(\frac{1}{4}x\right) $, we need to adjust these values:

At $ x = \pi $, the output becomes $ -2 $ (instead of 1).
At $ x = 3\pi $, the output becomes $ 2 $ (instead of -1).

Thus, the graph will be vertically stretched and flipped. The new points of interest are $ (\pi, -2) $ and $ (3\pi, 2) $. The graph will start from the lower left, rise to the point $ (2\pi, 0) $, and continue to the upper right, reflecting the periodic nature of the cotangent function.

In summary, the graph of $ y = -2 \cot\left(\frac{1}{4}x\right) $ will exhibit a period of $ 4\pi $, with asymptotes at $ x = 0, 4\pi, 8\pi $, and will be reflected over the x-axis with adjusted amplitude, resulting in a continuous wave-like pattern between the asymptotes.

Do you want more practice?

More sets

Graphs of Tangent and Cotangent Functions

4. Graphing Trigonometric Functions

4 problems

Topic

Patrick

4. Graphing Trigonometric Functions

4 topics 8 problems

Chapter

Patrick

Here’s what students ask on this topic:

What are the key characteristics of the tangent function graph?

The tangent function graph, derived from the identity $\tan (x) = \frac{\sin}{(}$ , has several key characteristics. It features vertical asymptotes at odd multiples of $\frac{π}{/}$ (e.g., $\frac{3}{π}$ , $\frac{5}{π}$ ). The period of the tangent function is $\frac{π}{/}$ , where $b$ is the coefficient of $x$ . The graph passes through the origin and repeats every $π$ units. It increases from negative infinity to positive infinity between each pair of asymptotes.

How do you graph the cotangent function?

To graph the cotangent function, recall that $\cot (x) = \frac{1}{/}$ . Start by identifying the vertical asymptotes, which occur at integer multiples of $π$ (e.g., $0$ , $π$ , $2 π$ ). The period of the cotangent function is $\frac{π}{/}$ , where $b$ is the coefficient of $x$ . The graph decreases from positive infinity to negative infinity between each pair of asymptotes. Plot points where the function crosses the x-axis, which occur at odd multiples of $\frac{π}{/}$ .

What is the period of the tangent and cotangent functions?

The period of the tangent and cotangent functions is $\frac{π}{/}$ , where $b$ is the coefficient of $x$ in the function. For example, if the function is $y = \tan (\frac{π}{/}$ , the period is $\frac{π}{/}$ , which simplifies to 2. This means the graph repeats every 2 units along the x-axis.

How do you determine the asymptotes of the tangent and cotangent functions?

The asymptotes of the tangent function occur at odd multiples of $\frac{π}{/}$ (e.g., $\frac{3}{π}$ , $\frac{5}{π}$ ). For the cotangent function, asymptotes occur at integer multiples of $π$ (e.g., $0$ , $π$ , $2 π$ ). These asymptotes are where the functions are undefined due to division by zero in their respective identities.

What are the differences between the tangent and cotangent graphs?

The tangent and cotangent graphs have several differences. The tangent graph has vertical asymptotes at odd multiples of $\frac{π}{/}$ , while the cotangent graph has asymptotes at integer multiples of $π$ . The tangent graph increases from negative infinity to positive infinity between asymptotes, whereas the cotangent graph decreases from positive infinity to negative infinity. Both graphs have a period of $\frac{π}{/}$ , but their shapes and asymptote locations differ.