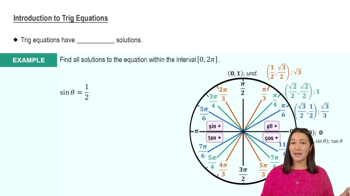
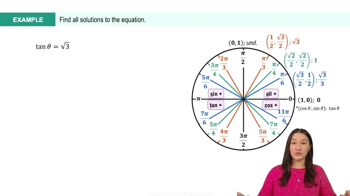
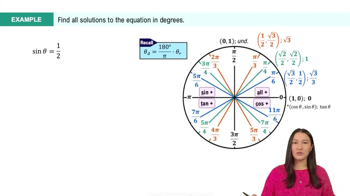
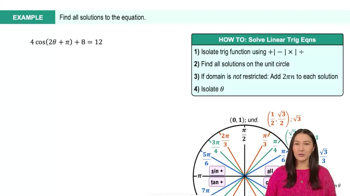
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
Practice this topic
- Multiple Choice
Find all solutions to the equation.
527views2rank - Multiple Choice
Find all solutions to the equation.
666views1rank - Multiple Choice
Find all solutions to the equation.
463views1rank - Multiple Choice
Find all solutions to the equation.
470views1rank - Textbook QuestionIn Exercises 1–10, use substitution to determine whether the given x-value is a solution of the equation. __ √ 2 𝝅cos x = ------- , x = ------ 2 4434views
- Textbook QuestionIn Exercises 1–10, use substitution to determine whether the given x-value is a solution of the equation. __ √ 3 𝝅sin x = ------- , x = ------- 2 6438views
- Textbook QuestionIn Exercises 1–10, use substitution to determine whether the given x-value is a solution of the equation. 1 2𝝅cos x = ﹣ ------- , x = --------- 2 3411views
- Textbook QuestionIn Exercises 1–10, use substitution to determine whether the given x-value is a solution of the equation. __ √ 3 5𝝅tan 2x = ﹣--------- , x = --------- 3 12463views