Angles in Standard Position: Study with Video Lessons, Practice Problems & Examples
Back to all problems
A sag curve in a highway is characterized by its downhill and then uphill direction. It must be properly designed to provide the drivers with the necessary safe stopping distance to avoid collision with any obstruction on the road. The minimum length, L, of a sag curve, depends on the height of the car's headlights, h, the downhill grade θ1 which is negative, the uphill grade θ2 which is positive, and the safe stopping distance, S, for a particular speed limit. Moreover, L depends on the angle of inclination of the headlights, α, with respect to the horizontal.
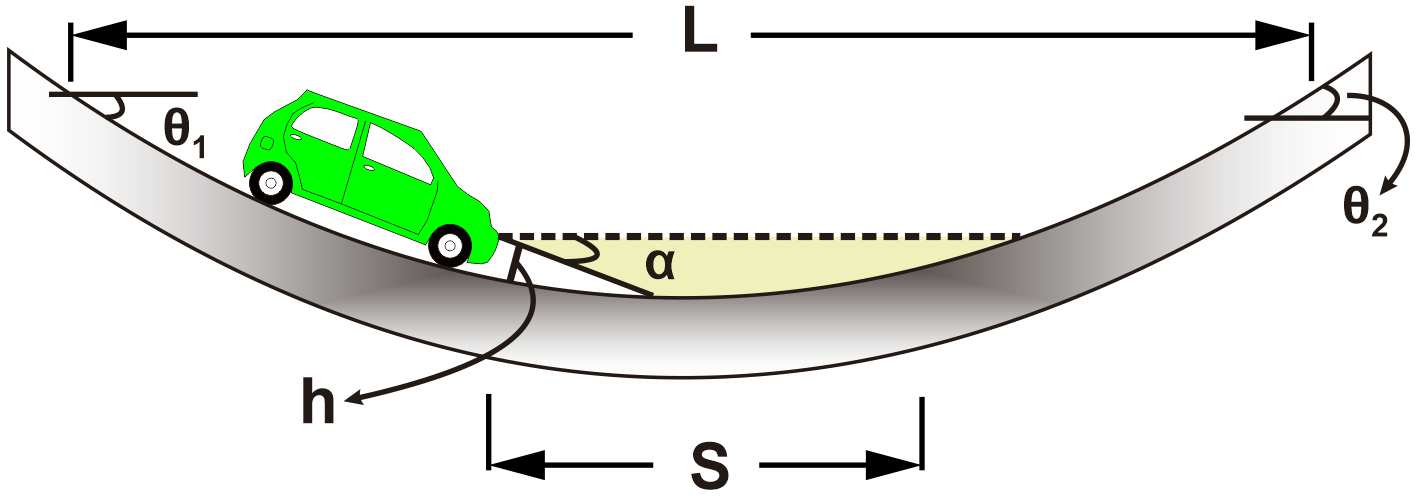
The following formula can be used for a 55 mph speed limit:
L = ((θ2 - θ1)S2)/(200(h + S tan α)), where S < L.
Note that the units for L, h, and S should be ft and all the angles should be in degrees.
For h = 1.7 ft, α = 0.7°, θ1 = -2°, θ2 = 5°, and S = 312 ft, calculate the length L to the nearest foot.
A sag curve in a highway is characterized by its downhill and then uphill direction. It must be properly designed to provide the drivers with the necessary safe stopping distance to avoid collision with any obstruction on the road. The minimum length, L, of a sag curve, depends on the height of the car's headlights, h, the downhill grade θ1 which is negative, the uphill grade θ2 which is positive, and the safe stopping distance, S, for a particular speed limit. Moreover, L depends on the angle of inclination of the headlights, α, with respect to the horizontal.
The following formula can be used for a 55 mph speed limit:
L = ((θ2 - θ1)S2)/(200(h + S tan α)), where S < L.
Note that the units for L, h, and S should be ft and all the angles should be in degrees.
For h = 1.7 ft, α = 0.7°, θ1 = -2°, θ2 = 5°, and S = 312 ft, calculate the length L to the nearest foot.