Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function Properties
The tangent function, defined as tan(x) = sin(x)/cos(x), has a periodic nature with a period of π. It exhibits vertical asymptotes where the cosine function equals zero, specifically at x = (π/2) + nπ for any integer n. Understanding these properties is crucial for analyzing the behavior of tangent graphs.
Recommended video:
Introduction to Tangent Graph
Phase Shift
Phase shift refers to the horizontal translation of a trigonometric function. For the tangent function, an equation of the form y = tan(x + c) indicates a leftward shift by c units, while y = tan(x - c) indicates a rightward shift. This concept is essential for determining how the graph of the tangent function is altered by changes in its equation.
Recommended video:
Vertical Asymptotes
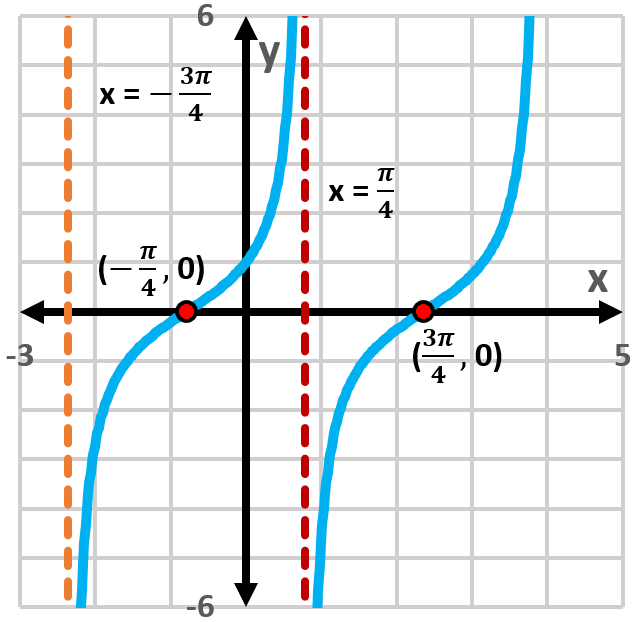
Vertical asymptotes in the graph of the tangent function occur at points where the function is undefined, specifically where cos(x) = 0. In the provided graph, the vertical asymptotes at x = -π/4 and x = π/4 indicate the boundaries of the function's behavior, where it approaches infinity. Identifying these asymptotes helps in selecting the correct equation for the graph.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 4:18m
4:18m