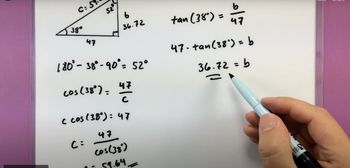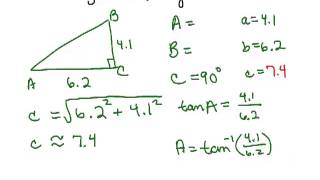Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
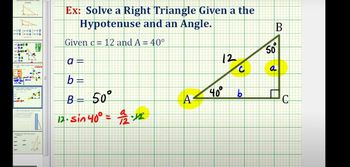
Solving Right Triangles
Problem 1a
Textbook Question
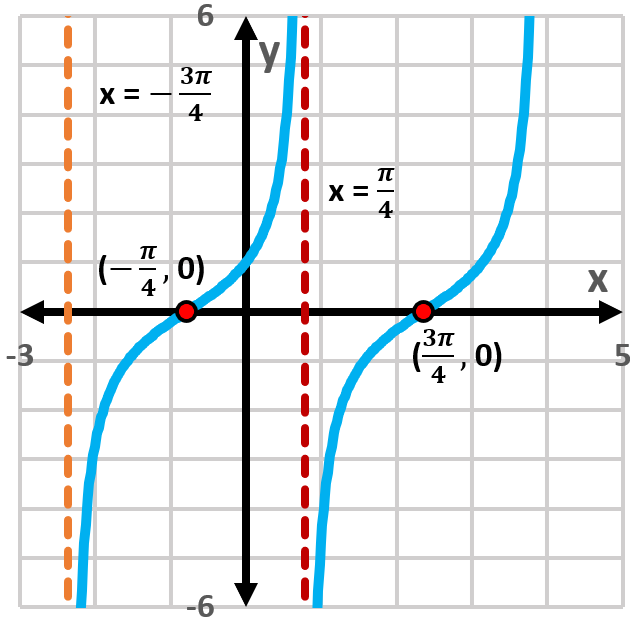
Textbook QuestionIn Exercises 1–4, the graph of a tangent function is given. Select the equation for each graph from the following options:
y = tan(x + π/2), y = tan(x + π), y = −tan(x − π/2).
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function Properties
The tangent function, defined as tan(x) = sin(x)/cos(x), has a periodic nature with a period of π. It exhibits vertical asymptotes where the cosine function equals zero, specifically at x = (π/2) + nπ for any integer n. Understanding these properties is crucial for analyzing the behavior of tangent graphs.
Recommended video:

Introduction to Tangent Graph
Phase Shift
Phase shift refers to the horizontal translation of a trigonometric function. For the tangent function, an equation of the form y = tan(x + c) indicates a leftward shift by c units, while y = tan(x - c) indicates a rightward shift. This concept is essential for determining how the graph of the tangent function is altered by changes in its equation.
Recommended video:
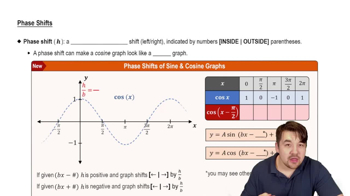
Phase Shifts
Vertical Asymptotes
Vertical asymptotes in the graph of the tangent function occur at points where the function is undefined, specifically where cos(x) = 0. In the provided graph, the vertical asymptotes at x = -π/4 and x = π/4 indicate the boundaries of the function's behavior, where it approaches infinity. Identifying these asymptotes helps in selecting the correct equation for the graph.
Recommended video:
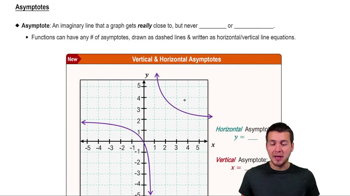
Asymptotes

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice