Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function
The tangent function, denoted as tan(x), is a periodic function defined as the ratio of the sine and cosine functions: tan(x) = sin(x)/cos(x). It has a period of π, meaning it repeats its values every π radians. The function has vertical asymptotes where the cosine function equals zero, specifically at odd multiples of π/2.
Recommended video:
Introduction to Tangent Graph
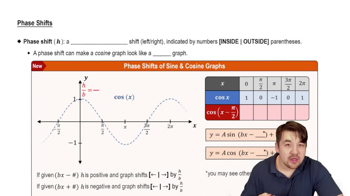
Phase Shift
A phase shift occurs when a function is horizontally shifted along the x-axis. In the function y = tan(x − π/4), the term (x − π/4) indicates a rightward shift of π/4 units. This transformation affects the starting point of the graph, altering where the function begins its periodic cycle.
Recommended video:
Graphing Trigonometric Functions
Graphing trigonometric functions involves plotting their values over a specified interval. For the tangent function, it is essential to identify key points, including the vertical asymptotes and the points where the function crosses the x-axis. For y = tan(x − π/4), one must consider the adjusted period and phase shift to accurately represent two complete cycles of the function.
Recommended video:
Introduction to Trigonometric Functions
 Verified Solution
Verified Solution


 4:18m
4:18m
