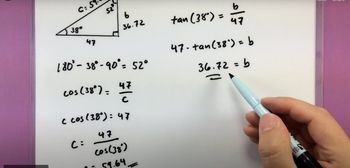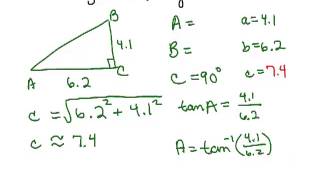Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
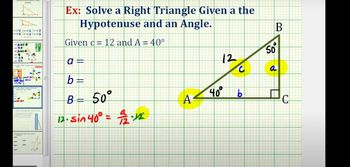
Solving Right Triangles
Problem 12
Textbook Question
In Exercises 5–12, graph two periods of the given tangent function. y = tan(x − π/4)
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Identify the basic form of the tangent function. The general form is y = a * tan(b(x - c)) + d, where a is the amplitude, b affects the period, c is the phase shift, and d is the vertical shift.>
<Step 2: Determine the period of the function. For y = tan(x), the period is π. Since there is no coefficient b affecting the x term, the period remains π.>
<Step 3: Identify the phase shift. The function is y = tan(x - π/4), which means there is a phase shift of π/4 to the right.>
<Step 4: Plot the asymptotes. For the basic tangent function, asymptotes occur at x = -π/2 and x = π/2. With the phase shift, these asymptotes move to x = -π/2 + π/4 and x = π/2 + π/4.>
<Step 5: Sketch the graph. Between each pair of asymptotes, the tangent function will pass through the origin of the shifted graph, which is now at (π/4, 0). Repeat this pattern to complete two periods of the graph.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function
The tangent function, denoted as tan(x), is a periodic function defined as the ratio of the sine and cosine functions: tan(x) = sin(x)/cos(x). It has a period of π, meaning it repeats its values every π radians. The function has vertical asymptotes where the cosine function equals zero, specifically at odd multiples of π/2.
Recommended video:

Introduction to Tangent Graph
Phase Shift
A phase shift occurs when a function is horizontally shifted along the x-axis. In the function y = tan(x − π/4), the term (x − π/4) indicates a rightward shift of π/4 units. This transformation affects the starting point of the graph, altering where the function begins its periodic cycle.
Recommended video:
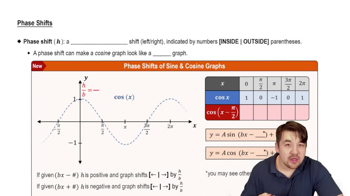
Phase Shifts
Graphing Trigonometric Functions
Graphing trigonometric functions involves plotting their values over a specified interval. For the tangent function, it is essential to identify key points, including the vertical asymptotes and the points where the function crosses the x-axis. For y = tan(x − π/4), one must consider the adjusted period and phase shift to accurately represent two complete cycles of the function.
Recommended video:

Introduction to Trigonometric Functions

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice