Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Trigonometric Functions on Right Triangles
Problem 45b
Textbook Question
Determine whether each statement is possible or impossible. b. tan θ = 1.4
 Verified step by step guidance
Verified step by step guidance1
insert step 1> Identify the range of the tangent function. The tangent function, \( \tan \theta \), can take any real number value from \(-\infty\) to \(+\infty\).
insert step 2> Recognize that \( \tan \theta = 1.4 \) is a real number.
insert step 3> Since 1.4 is within the range of possible values for the tangent function, the statement \( \tan \theta = 1.4 \) is possible.
insert step 4> Consider the unit circle or the tangent graph to visualize that \( \tan \theta \) can indeed equal 1.4 at some angle \( \theta \).
insert step 5> Conclude that the statement is possible because the tangent function can take any real number value, including 1.4.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
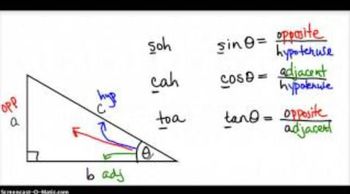
Tangent Function
The tangent function, denoted as tan(θ), is a fundamental trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. It can also be expressed as tan(θ) = sin(θ) / cos(θ). The range of the tangent function is all real numbers, meaning it can take any value, including positive values like 1.4.
Recommended video:

Introduction to Tangent Graph
Angle Measurement
Angles in trigonometry can be measured in degrees or radians. The tangent function is periodic with a period of π radians (or 180 degrees), which means that for any angle θ, tan(θ) = tan(θ + nπ) for any integer n. This periodicity allows for multiple angles to yield the same tangent value, including 1.4.
Recommended video:

Reference Angles on the Unit Circle
Existence of Solutions
In trigonometry, a statement like tan(θ) = 1.4 is possible because the tangent function can produce any real number as an output. Therefore, there exist angles θ for which this equation holds true. Specifically, one can find angles in both the first and third quadrants that satisfy this condition.
Recommended video:

Intro to Complementary & Supplementary Angles

 6:4m
6:4mWatch next
Master Introduction to Trigonometric Functions with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice