Textbook Question
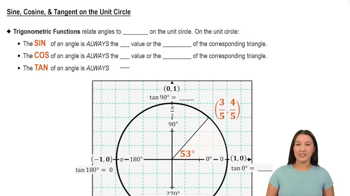
CONCEPT PREVIEW Fill in the blank(s) to correctly complete each sentence. Given tan θ = 1/cot θ , two equivalent forms of this identity are cot θ = 1/______ and tan θ . ______ = 1 .
761
views
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: