Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Solving Right Triangles
Problem 23b
Textbook Question
In Exercises 17–24, graph two periods of the given cotangent function. y = 3 cot(x + π/2)
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Identify the basic form of the cotangent function. The general form is y = a \cdot \cot(bx + c) + d. In this case, a = 3, b = 1, c = \frac{\pi}{2}, and d = 0.>
<Step 2: Determine the period of the function. The period of the cotangent function is given by \frac{\pi}{|b|}. Since b = 1, the period is \pi.>
<Step 3: Identify the phase shift. The phase shift is given by -\frac{c}{b}. Here, c = \frac{\pi}{2} and b = 1, so the phase shift is -\frac{\pi}{2}. This means the graph is shifted \frac{\pi}{2} units to the left.>
<Step 4: Determine the vertical stretch/compression and reflection. The coefficient a = 3 indicates a vertical stretch by a factor of 3. There is no reflection since a is positive.>
<Step 5: Sketch the graph. Start by plotting key points for one period, considering the phase shift and vertical stretch. Then, replicate this pattern to complete two periods of the graph.>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Cotangent Function
The cotangent function, denoted as cot(x), is the reciprocal of the tangent function. It is defined as cot(x) = cos(x)/sin(x). The cotangent function has a period of π, meaning it repeats its values every π units along the x-axis. Understanding its behavior, including asymptotes and zeros, is crucial for graphing.
Recommended video:

Introduction to Cotangent Graph
Phase Shift
Phase shift refers to the horizontal translation of a trigonometric function. In the function y = 3 cot(x + π/2), the term (x + π/2) indicates a leftward shift of π/2 units. This shift alters the starting point of the graph, affecting where the function's key features, such as asymptotes and intercepts, occur.
Recommended video:
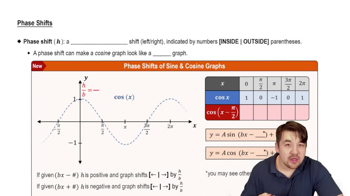
Phase Shifts
Amplitude and Vertical Stretch
In the function y = 3 cot(x + π/2), the coefficient 3 represents a vertical stretch of the cotangent function. While cotangent does not have an amplitude in the traditional sense (as it extends to infinity), this factor affects the steepness of the graph. Understanding how vertical scaling influences the graph's appearance is essential for accurate representation.
Recommended video:

Stretches and Shrinks of Functions

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice