Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
5. Inverse Trigonometric Functions and Basic Trigonometric Equations
Linear Trigonometric Equations
Problem 17
Textbook Question
Textbook QuestionIn Exercises 11–24, find all solutions of each equation. tan x = 0
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
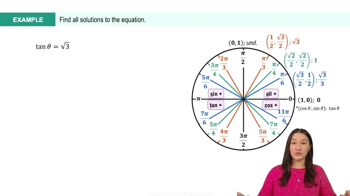
Tangent Function
The tangent function, denoted as tan(x), is a fundamental trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. It can also be expressed as tan(x) = sin(x)/cos(x). Understanding the behavior of the tangent function, including its periodicity and asymptotes, is crucial for solving equations involving it.
Recommended video:

Introduction to Tangent Graph
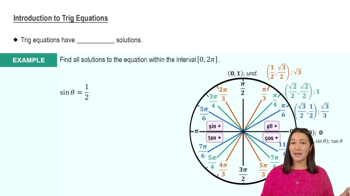
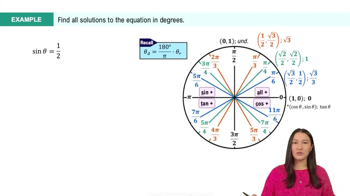
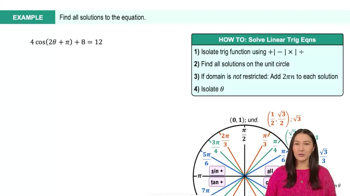
Solutions of Trigonometric Equations
Trigonometric equations often have multiple solutions due to the periodic nature of trigonometric functions. For example, the equation tan(x) = 0 has solutions at specific angles where the tangent function crosses the x-axis. Recognizing that these solutions repeat every π radians is essential for finding all possible solutions.
Recommended video:

How to Solve Linear Trigonometric Equations
Unit Circle
The unit circle is a circle with a radius of one centered at the origin of a coordinate plane. It is a vital tool in trigonometry for understanding the values of sine, cosine, and tangent at various angles. By analyzing the unit circle, one can easily determine the angles where tan(x) = 0, specifically at integer multiples of π.
Recommended video:

Introduction to the Unit Circle

 4:25m
4:25mWatch next
Master Introduction to Trig Equations with a bite sized video explanation from Callie Rethman
Start learning