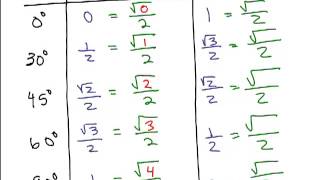Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
Special Right Triangles
Problem 6
Textbook Question
Match each trigonometric function in Column I with its value in Column II. Choices may be used once, more than once, or not at all.
cot 30°
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recall the definition of the cotangent function. Cotangent is the reciprocal of the tangent function, so \( \cot \theta = \frac{1}{\tan \theta} \).
Step 2: Identify the tangent of 30°. From trigonometric tables or the unit circle, \( \tan 30° = \frac{1}{\sqrt{3}} \).
Step 3: Use the reciprocal relationship to find \( \cot 30° \). Since \( \cot 30° = \frac{1}{\tan 30°} \), substitute the value of \( \tan 30° \) into the equation.
Step 4: Simplify the expression \( \cot 30° = \frac{1}{\frac{1}{\sqrt{3}}} \).
Step 5: Simplify further to find \( \cot 30° = \sqrt{3} \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
Trigonometric functions relate the angles of a triangle to the lengths of its sides. The primary functions include sine, cosine, tangent, cotangent, secant, and cosecant. Each function has specific definitions based on a right triangle or the unit circle, which are essential for calculating values associated with angles.
Recommended video:

Introduction to Trigonometric Functions
Cotangent Function
The cotangent function, denoted as cot(θ), is the reciprocal of the tangent function. It is defined as the ratio of the adjacent side to the opposite side in a right triangle. For example, cot(30°) can be calculated as 1/tan(30°), which helps in determining its value using known trigonometric ratios.
Recommended video:

Introduction to Cotangent Graph
Special Angles in Trigonometry
Certain angles, such as 30°, 45°, and 60°, are known as special angles in trigonometry because their sine, cosine, and tangent values are well-defined and can be easily memorized. For instance, cot(30°) corresponds to a specific value derived from the properties of a 30-60-90 triangle, making it straightforward to compute.
Recommended video:

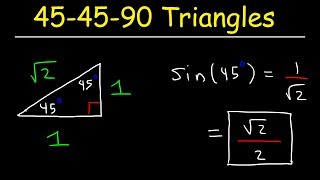
45-45-90 Triangles

 4:34m
4:34mWatch next
Master 45-45-90 Triangles with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice