Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
4. Graphing Trigonometric Functions
Graphs of the Sine and Cosine Functions
Problem 80
Textbook Question
Textbook QuestionIn Exercises 79–82, graph f, g, and h in the same rectangular coordinate system for 0 ≤ x ≤ 2π. Obtain the graph of h by adding or subtracting the corresponding y-coordinates on the graphs of f and g. f(x) = 2 cos x, g(x) = cos 2x, h(x) = (f + g)(x)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
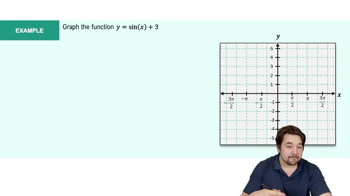
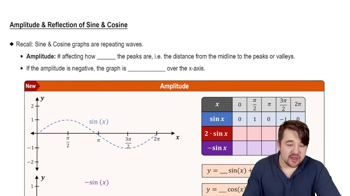
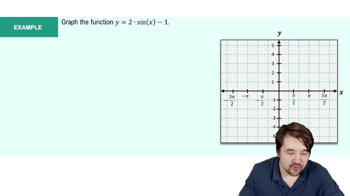
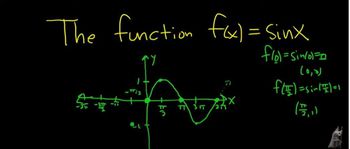
Trigonometric functions, such as sine and cosine, are fundamental in trigonometry, representing relationships between angles and sides of triangles. In this context, f(x) = 2 cos x and g(x) = cos 2x are specific trigonometric functions that will be graphed. Understanding their periodic nature and amplitude is crucial for accurately plotting their graphs.
Recommended video:

Introduction to Trigonometric Functions
Graphing Functions
Graphing functions involves plotting points on a coordinate system to visualize the behavior of the function over a specified interval. For the given functions f and g, it is essential to determine key features such as intercepts, maxima, minima, and periodicity. This visual representation aids in understanding how the functions interact when combined to form h(x).
Recommended video:

Graph of Sine and Cosine Function
Function Addition and Subtraction
The process of adding or subtracting functions involves combining their outputs for corresponding inputs. In this case, h(x) = (f + g)(x) means that for each x-value, the y-coordinates of f and g are added together. This concept is vital for determining the resulting graph of h, as it reflects the combined effects of the individual functions on the overall output.
Recommended video:

Adding and Subtracting Complex Numbers

 5:53m
5:53mWatch next
Master Graph of Sine and Cosine Function with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice