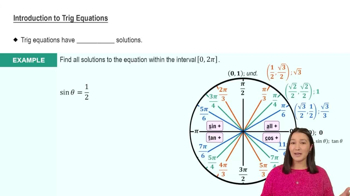
In Exercises 53–62, solve each equation on the interval [0, 2𝝅). cot x (tan x - 1) = 0

Verified step by step guidance

1. Recognize that the equation is a product of two factors: \( \cot x \) and \( (\tan x - 1) \). For the product to be zero, at least one of these factors must be zero.
2. Set the first factor equal to zero: \( \cot x = 0 \). Recall that \( \cot x = \frac{1}{\tan x} \), so this implies \( \tan x \) is undefined. Determine the values of \( x \) where \( \tan x \) is undefined within the interval \([0, 2\pi)\).
3. Set the second factor equal to zero: \( \tan x - 1 = 0 \). Solve for \( x \) by finding where \( \tan x = 1 \).
4. Identify the angles \( x \) within the interval \([0, 2\pi)\) where \( \tan x = 1 \). These are the angles where the tangent function has a value of 1.
5. Combine the solutions from both factors to find all values of \( x \) that satisfy the original equation within the given interval.

Key Concepts

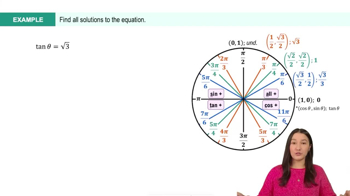
Cotangent and Tangent Functions

The cotangent (cot) and tangent (tan) functions are fundamental trigonometric functions defined as cot(x) = cos(x)/sin(x) and tan(x) = sin(x)/cos(x), respectively. Understanding these functions is crucial for solving equations involving them, as they relate angles to the ratios of the sides of a right triangle. Their periodic nature and specific values at key angles (like 0, π/4, and π/2) are essential for finding solutions within a given interval.

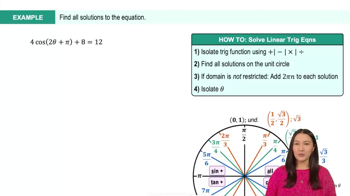
Zero Product Property

The Zero Product Property states that if the product of two factors equals zero, at least one of the factors must be zero. This principle is vital for solving equations like cot(x)(tan(x) - 1) = 0, as it allows us to set each factor to zero separately. By applying this property, we can simplify the problem into smaller, more manageable equations that can be solved individually.

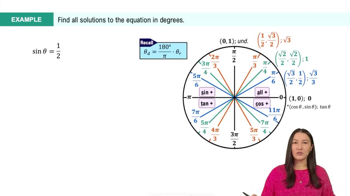
Interval Notation and Solutions

Interval notation specifies the range of values for which a function or equation is defined or valid. In this case, the interval [0, 2π) indicates that we are looking for solutions within one full rotation of the unit circle, excluding 2π. Understanding how to interpret and apply this notation is crucial for determining valid solutions to trigonometric equations, ensuring that all answers fall within the specified range.