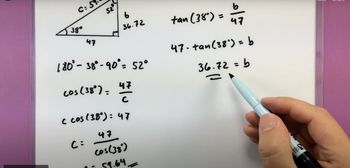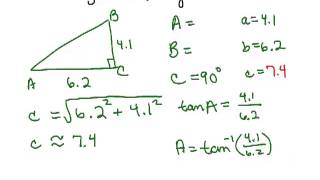Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
2. Trigonometric Functions on Right Triangles
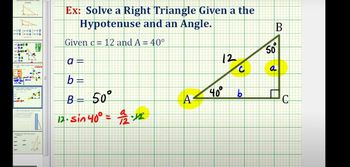
Solving Right Triangles
Problem 5a
Textbook Question
Textbook QuestionIn Exercises 5–12, graph two periods of the given tangent function. y = 3 tan x/4
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function
The tangent function, denoted as tan(x), is a fundamental trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. It is periodic with a period of π, meaning it repeats its values every π radians. Understanding the basic shape and properties of the tangent function is essential for graphing transformations.
Recommended video:

Introduction to Tangent Graph
Transformations of Functions
Transformations involve changing the position or shape of a function's graph. In the given function y = 3 tan(x/4), the coefficient '3' vertically stretches the graph by a factor of 3, while 'x/4' indicates a horizontal stretch, increasing the period to 4π. Recognizing these transformations helps in accurately sketching the graph.
Recommended video:

Domain and Range of Function Transformations
Graphing Periodic Functions
Graphing periodic functions like the tangent function requires understanding their key features, including asymptotes, intercepts, and periodicity. For the tangent function, vertical asymptotes occur where the function is undefined, specifically at odd multiples of π/2. Knowing how to identify these features is crucial for accurately graphing two periods of the function.
Recommended video:

Period of Sine and Cosine Functions

 4:18m
4:18mWatch next
Master Finding Missing Side Lengths with a bite sized video explanation from Nick Kaneko
Start learningRelated Videos
Related Practice