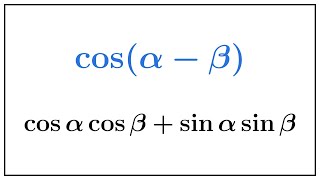Table of contents
- 0. Review of College Algebra4h 43m
- 1. Measuring Angles39m
- 2. Trigonometric Functions on Right Triangles2h 5m
- 3. Unit Circle1h 19m
- 4. Graphing Trigonometric Functions1h 19m
- 5. Inverse Trigonometric Functions and Basic Trigonometric Equations1h 41m
- 6. Trigonometric Identities and More Equations2h 34m
- 7. Non-Right Triangles1h 38m
- 8. Vectors2h 25m
- 9. Polar Equations2h 5m
- 10. Parametric Equations1h 6m
- 11. Graphing Complex Numbers1h 7m
6. Trigonometric Identities and More Equations
Sum and Difference Identities
Problem 5.16b
Textbook Question
Find the exact value of each expression.
tan (5π/12)
 Verified step by step guidance
Verified step by step guidance1
Recognize that \( \frac{5\pi}{12} \) can be expressed as a sum of angles whose tangent values are known, such as \( \frac{\pi}{4} + \frac{\pi}{6} \).
Use the tangent addition formula: \( \tan(a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b} \).
Substitute \( a = \frac{\pi}{4} \) and \( b = \frac{\pi}{6} \) into the formula.
Calculate \( \tan \frac{\pi}{4} = 1 \) and \( \tan \frac{\pi}{6} = \frac{1}{\sqrt{3}} \).
Substitute these values into the formula to find \( \tan \left( \frac{5\pi}{12} \right) = \frac{1 + \frac{1}{\sqrt{3}}}{1 - 1 \cdot \frac{1}{\sqrt{3}}} \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
0m:0sPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Tangent Function
The tangent function, denoted as tan(θ), is a fundamental trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. It can also be expressed in terms of sine and cosine as tan(θ) = sin(θ)/cos(θ). Understanding the properties and values of the tangent function is essential for solving trigonometric expressions.
Recommended video:

Introduction to Tangent Graph
Angle Addition Formula
The angle addition formula for tangent states that tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b)). This formula allows us to find the tangent of angles that are sums of known angles, which is particularly useful for calculating values like tan(5π/12) by expressing it as the sum of angles such as π/3 and π/4.
Recommended video:

Quadratic Formula
Exact Values of Trigonometric Functions
Exact values of trigonometric functions refer to the specific values of sine, cosine, and tangent for commonly used angles, such as 0, π/6, π/4, π/3, and π/2. These values can be derived from the unit circle or special triangles. Knowing these exact values is crucial for simplifying expressions and solving trigonometric equations accurately.
Recommended video:

Introduction to Trigonometric Functions

 6:14m
6:14mWatch next
Master Sum and Difference of Sine & Cosine with a bite sized video explanation from Callie Rethman
Start learningRelated Videos
Related Practice