Quadratic Functions: Videos & Practice Problems

Quadratic functions, expressed in standard form as f(x) = a(x-h)² + k, exhibit a parabolic shape. Key features include the vertex, axis of symmetry, and intercepts. The vertex indicates minimum or maximum points, while the axis of symmetry is x = h. Understanding transformations through parameters a, h, and k aids in graphing.

Properties of Parabolas

Quadratic functions are a specific type of polynomial function characterized by their degree of 2. The standard form of a quadratic function is expressed as \( f(x) = ax^2 + bx + c \), where \( a \), \( b \), and \( c \) are real numbers, and \( a \) cannot be zero. The graph of any quadratic function takes the shape of a parabola, which can open either upward or downward depending on the sign of \( a \).

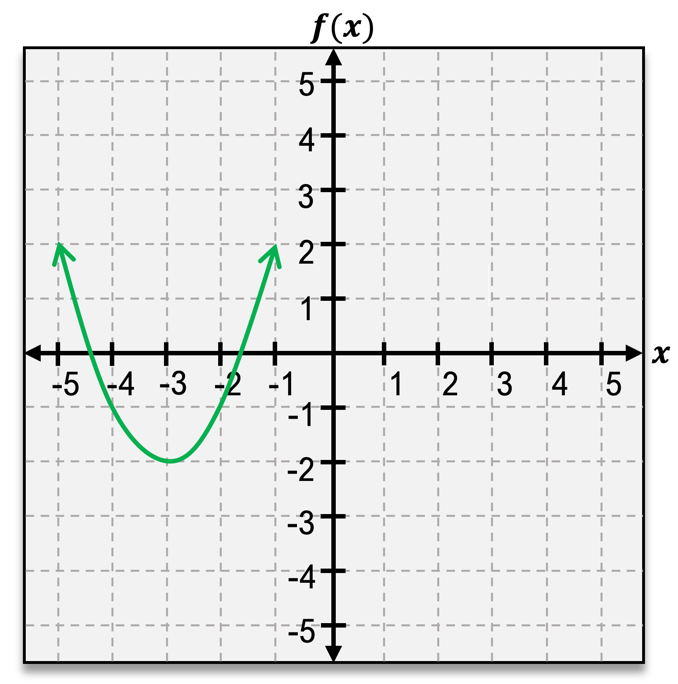
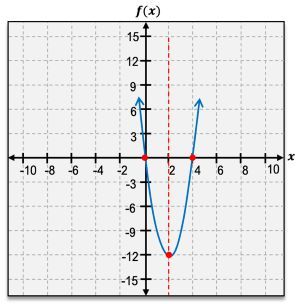
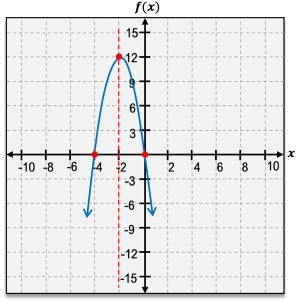
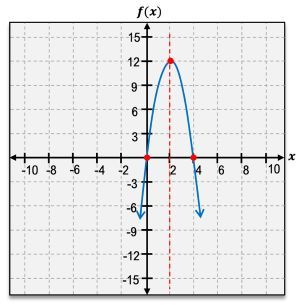
The vertex of a parabola is a crucial feature, representing either the highest or lowest point on the graph. If the parabola opens upward, the vertex is a minimum point; if it opens downward, the vertex is a maximum point. The vertex is denoted as an ordered pair, such as \( (h, k) \), where \( h \) and \( k \) are the x and y coordinates, respectively.

Another important aspect of quadratic functions is the x-intercepts, which are the points where the graph crosses the x-axis. A quadratic function can have either one or two x-intercepts, but never more. The y-intercept, on the other hand, is where the graph intersects the y-axis, and it can be found by evaluating \( f(0) \).

The axis of symmetry is a vertical line that divides the parabola into two mirror-image halves, always passing through the vertex. It can be expressed as \( x = h \), where \( h \) is the x-coordinate of the vertex.

When analyzing the domain and range of quadratic functions, the domain is always all real numbers, represented as \( (-\infty, \infty) \). The range, however, depends on whether the vertex is a minimum or maximum. For a minimum vertex, the range extends from the vertex's y-coordinate to infinity, while for a maximum vertex, it extends from negative infinity to the vertex's y-coordinate.

Additionally, understanding the intervals of increase and decrease is essential. A parabola increases on the interval from negative infinity to the vertex and decreases from the vertex to positive infinity. This behavior is determined by the vertex's position on the graph.

Quadratic functions can also be expressed in vertex form, which is particularly useful for graphing. The vertex form is given by \( f(x) = a(x - h)^2 + k \), where \( (h, k) \) is the vertex of the parabola. This form allows for easier identification of the vertex and the direction in which the parabola opens.

Identify the ordered pair of the vertex of the parabola. State whether it is a minimum or maximum.

• A. $\left(-3,-2\right);$ maximum
• B. $\left(-3,-2\right);$ minimum
• C. $\left(-1,2\right);$ maximum
• D. $\left(-1,2\right);$ minimum

Answer: (B)

Where is the axis of symmetry located on the given parabola? 

• A. $x=3$
• B. $x=0$
• C. $x=1$
• D. $x=4$

Answer: (A)

Vertex Form

Understanding the vertex form of a quadratic function is essential for graphing parabolas effectively. The vertex form is expressed as:

$$f(x) = a(x - h)^2 + k$$

In this equation, the parameters \(a\), \(h\), and \(k\) represent specific transformations of the basic quadratic function \(f(x) = x^2\). The value of \(a\) determines the direction and width of the parabola. If \(a\) is positive, the parabola opens upwards, while a negative \(a\) indicates it opens downwards. The absolute value of \(a\) also affects the shape: if \(|a| > 1\), the parabola undergoes a vertical stretch, making it narrower; if \(|a| < 1\), it experiences a vertical compression, resulting in a wider shape.

The parameter \(h\) indicates a horizontal shift. Since the equation is \(x - h\), a positive \(h\) shifts the graph to the right, while a negative \(h\) shifts it to the left. The parameter \(k\) represents a vertical shift, where a positive \(k\) moves the graph up and a negative \(k\) moves it down.

To graph a quadratic function in vertex form, follow these steps:

1. **Identify the Vertex**: The vertex of the parabola is given by the point \((h, k)\). For example, if \(h = 1\) and \(k = -4\), the vertex is at \((1, -4)\).

2. **Determine the Axis of Symmetry**: The axis of symmetry is the vertical line that passes through the vertex, expressed as \(x = h\). In our example, the axis of symmetry is \(x = 1\).

3. **Find the X-Intercepts**: To find the x-intercepts, set \(f(x) = 0\) and solve for \(x\). This often involves rearranging the equation into a solvable form, such as using the square root property. For instance, if you have \(f(x) = (x - 1)^2 - 4\), setting it to zero gives you \(x - 1 = \pm 2\), leading to intercepts at \(x = 3\) and \(x = -1\).

4. **Calculate the Y-Intercept**: The y-intercept is found by evaluating \(f(0)\). Plugging in \(0\) for \(x\) in the vertex form allows you to compute the y-coordinate of the intercept. For example, if \(f(0) = (0 - 1)^2 - 4\), this results in \(f(0) = -3\), giving a y-intercept at \((0, -3)\).

5. **Plot the Points and Draw the Parabola**: With the vertex, axis of symmetry, x-intercepts, and y-intercept identified, plot these points on a coordinate plane. Connect them with a smooth curve, ensuring the shape reflects that of a parabola, and add arrows at the ends to indicate that the graph continues indefinitely.

By following these steps, you can accurately graph any quadratic function in vertex form, utilizing the transformations represented by \(a\), \(h\), and \(k\) to visualize the function's behavior effectively.

Example 1

To graph the quadratic function f(x) = -\frac{1}{2}(x + 1)^2 + 2, we start by identifying key features of the parabola. The function is in vertex form, which is expressed as f(x) = a(x - h)^2 + k, where (h, k) represents the vertex. In this case, we can rewrite the function to find the vertex:

Here, x + 1 can be interpreted as x - (-1), indicating that h = -1 and k = 2. Thus, the vertex is located at the point (-1, 2). Since the coefficient a = -\frac{1}{2} is negative, the parabola opens downward, confirming that the vertex is a maximum point.

The axis of symmetry for the parabola is given by the line x = h, which in this case is x = -1.

Next, we find the x-intercepts by setting f(x) = 0:

-\frac{1}{2}(x + 1)^2 + 2 = 0

Rearranging gives:

-\frac{1}{2}(x + 1)^2 = -2

Multiplying both sides by -2 results in:

(x + 1)^2 = 4

Taking the square root of both sides yields:

x + 1 = \pm 2

Solving for x gives two x-intercepts: x = 1 and x = -3.

To find the y-intercept, we evaluate f(0):

f(0) = -\frac{1}{2}(0 + 1)^2 + 2 = -\frac{1}{2}(1) + 2 = -\frac{1}{2} + 2 = \frac{3}{2}

Thus, the y-intercept is (0, \frac{3}{2}).

With the vertex (-1, 2), x-intercepts (1, 0) and (-3, 0), and y-intercept (0, \frac{3}{2}), we can plot these points on a graph. The parabola will be symmetric about the line x = -1.

The domain of any quadratic function is all real numbers, expressed as (-\infty, \infty). The range, however, is determined by the maximum point at the vertex, which is y ≤ 2. Therefore, the range is (-\infty, 2].

For increasing and decreasing intervals, the function increases from (-\infty, -1) and decreases from (-1, \infty). The vertex at x = -1 is not included in the increasing or decreasing intervals as it represents the transition point.

In summary, the key features of the quadratic function are:

• Vertex: (-1, 2) (maximum point)
• Axis of symmetry: x = -1
• X-intercepts: (1, 0) and (-3, 0)
• Y-intercept: (0, \frac{3}{2})
• Domain: (-\infty, \infty)
• Range: (-\infty, 2]
• Increasing interval: (-\infty, -1)
• Decreasing interval: (-1, \infty)

With this information, you can accurately graph the quadratic function and analyze its characteristics.

Graph the given quadratic function. Identify the vertex, axis of symmetry, intercepts, domain, range, and intervals for which the function is increasing or decreasing. $f\left(x\right)=-\left(x-5\right)^2+1$

• A.
• B.
• C.
• D.

Answer: (A)

Converting Standard Form to Vertex Form

When working with quadratic functions, it's essential to understand how to convert a function from standard form to vertex form, especially when you want to identify the vertex and intercepts for graphing. The vertex form of a quadratic function is expressed as \( f(x) = a(x - h)^2 + k \), where \( (h, k) \) represents the vertex of the parabola. If you start with a quadratic in standard form, such as \( f(x) = ax^2 + bx + c \), you can transform it into vertex form by completing the square.

To illustrate this process, consider the function \( f(x) = x^2 + 6x + 7 \). First, identify the coefficients: \( a = 1 \), \( b = 6 \), and \( c = 7 \). The first step is to factor out \( a \) from the first two terms. Since \( a \) is 1, this step simplifies to \( x^2 + 6x \).

Next, to complete the square, calculate \( \frac{b}{2a} \). Here, \( \frac{6}{2 \cdot 1} = 3 \). Squaring this value gives \( 3^2 = 9 \). You then add and subtract this square inside the parentheses: \( x^2 + 6x + 9 - 9 + 7 \). This manipulation allows you to maintain the equality of the function while preparing to factor.

Now, factor the perfect square trinomial \( x^2 + 6x + 9 \) into \( (x + 3)^2 \). The expression now looks like \( (x + 3)^2 - 2 \) after combining the constants \( -9 + 7 \). This final form, \( f(x) = (x + 3)^2 - 2 \), is in vertex form, where the vertex \( (h, k) \) is \( (-3, -2) \).

With the function in vertex form, you can easily graph it. The vertex provides a starting point, and from there, you can determine the x and y intercepts. This method of completing the square is a powerful tool for transforming quadratic functions and understanding their graphical representations.

Example 2

To analyze the quadratic function f(x) = -2x² - 4x + 6, we will convert it from standard form to vertex form by completing the square. This process simplifies graphing and helps identify key features of the parabola.

First, we identify the coefficients: a = -2, b = -4, and c = 6. The first step in completing the square is to factor out a from the first two terms:

f(x) = -2(x² + 2x) + 6

Next, we calculate b/(2a) to find the value needed to complete the square:

b/(2a) = -4/(2 * -2) = 1

We then add and subtract this value squared (1) inside the parentheses:

f(x) = -2(x² + 2x + 1 - 1) + 6

Now, we can move the subtracted term outside the parentheses:

f(x) = -2((x + 1)² - 1) + 6

This simplifies to:

f(x) = -2(x + 1)² + 2 + 6 = -2(x + 1)² + 8

Now, we have the vertex form of the function: f(x) = -2(x + 1)² + 8. The vertex of the parabola is at the point (h, k) = (-1, 8). Since the coefficient of the squared term is negative, the parabola opens downwards, indicating that the vertex is a maximum point.

The axis of symmetry can be determined from the vertex, which is the line x = -1.

Next, we find the x-intercepts by setting f(x) = 0:

-2(x + 1)² + 8 = 0

Rearranging gives:

-2(x + 1)² = -8

Dividing by -2 results in:

(x + 1)² = 4

Taking the square root of both sides yields:

x + 1 = ±2

Thus, the solutions are:

x = -1 + 2 = 1 and x = -1 - 2 = -3

So, the x-intercepts are at (1, 0) and (-3, 0).

To find the y-intercept, we evaluate f(0):

f(0) = -2(0 + 1)² + 8 = -2(1) + 8 = 6

Thus, the y-intercept is at (0, 6).

Now we can summarize the key features of the parabola:

• Vertex: (-1, 8)
• Axis of Symmetry: x = -1
• X-Intercepts: (1, 0) and (-3, 0)
• Y-Intercept: (0, 6)
• Domain: (-∞, ∞)
• Range: (-∞, 8]
• Increasing Interval: (-∞, -1)
• Decreasing Interval: (-1, ∞)

With this information, we can graph the parabola, ensuring to plot the vertex, intercepts, and axis of symmetry, and connect these points with a smooth curve to represent the downward-opening parabola.

Graph the given quadratic function. Identify the vertex, axis of symmetry, intercepts, domain, range, and intervals for which the function is increasing or decreasing. $f\left(x\right)=3x^2+12x$

• A.
• B.
• C.
• D.

Answer: (C)

Here’s what students ask on this topic:

What is the standard form of a quadratic function?

The standard form of a quadratic function is given by:

$f\left(x\right)=a{x}^2+bx+c$

where $a$, $b$, and $c$ are real numbers, and $a$ ≠ 0. This form is useful for identifying the coefficients that affect the shape and position of the parabola on the coordinate plane.

How do you find the vertex of a quadratic function in standard form?

To find the vertex of a quadratic function in standard form $f\left(x\right)=a{x}^2+bx+c$, use the formula:

$x=-b/\left(2a\right)$

This gives the x-coordinate of the vertex. To find the y-coordinate, substitute this x value back into the original function:

$y=f(-b/(2a\left)\right)$

The vertex is then $(-b/(2a),f(-b/\left(2a\right)\left)\right)$.

What is the vertex form of a quadratic function?

The vertex form of a quadratic function is:

$f\left(x\right)=a(x-h{)}^2+k$

where $a$ determines the direction and width of the parabola, and $h$ and $k$ are the coordinates of the vertex. This form is particularly useful for graphing because it directly shows the vertex and the transformations applied to the basic parabola $y=x^2$.

How do you convert a quadratic function from standard form to vertex form?

To convert a quadratic function from standard form $f\left(x\right)=a{x}^2+bx+c$ to vertex form $f\left(x\right)=a(x-h{)}^2+k$, follow these steps:

1. Factor out $a$ from the first two terms.

2. Complete the square inside the parentheses.

3. Add and subtract the same value inside the parentheses, then move the subtracted value outside.

4. Simplify to get the vertex form.

This process involves algebraic manipulation to rewrite the quadratic in a form that reveals the vertex directly.

What is the axis of symmetry in a quadratic function?

The axis of symmetry of a quadratic function is a vertical line that passes through the vertex of the parabola. For a quadratic function in vertex form $f\left(x\right)=a(x-h{)}^2+k$, the axis of symmetry is given by the equation:

$x=h$

This line divides the parabola into two mirror-image halves, ensuring that the function is symmetric about this line.