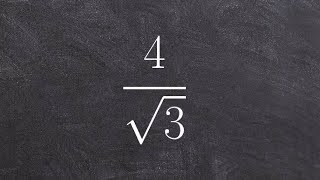Table of contents
- 0. Fundamental Concepts of Algebra3h 29m
- 1. Equations and Inequalities3h 27m
- 2. Graphs1h 43m
- 3. Functions & Graphs2h 17m
- 4. Polynomial Functions1h 54m
- 5. Rational Functions1h 23m
- 6. Exponential and Logarithmic Functions2h 28m
- 7. Measuring Angles40m
- 8. Trigonometric Functions on Right Triangles2h 5m
- 9. Unit Circle1h 19m
- 10. Graphing Trigonometric Functions1h 19m
- 11. Inverse Trigonometric Functions and Basic Trig Equations1h 41m
- 12. Trigonometric Identities 2h 34m
- 13. Non-Right Triangles1h 38m
- 14. Vectors2h 25m
- 15. Polar Equations2h 5m
- 16. Parametric Equations1h 6m
- 17. Graphing Complex Numbers1h 7m
- 18. Systems of Equations and Matrices3h 6m
- 19. Conic Sections2h 36m
- 20. Sequences, Series & Induction1h 15m
- 21. Combinatorics and Probability1h 45m
- 22. Limits & Continuity1h 49m
- 23. Intro to Derivatives & Area Under the Curve2h 9m
0. Fundamental Concepts of Algebra
Rationalize Denominator
Struggling with Precalculus?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
Rationalize the denominator and simplify the radical expression.
2+32−3
A
7−43
B
7+431
C
7+43
D
7−431
 Verified step by step guidance
Verified step by step guidance1
Identify the expression to be rationalized: \( \frac{2 - \sqrt{3}}{2 + \sqrt{3}} \). The goal is to eliminate the square root in the denominator.
Multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of \(2 + \sqrt{3}\) is \(2 - \sqrt{3}\).
Perform the multiplication: \( (2 - \sqrt{3})(2 - \sqrt{3}) \) for the numerator and \( (2 + \sqrt{3})(2 - \sqrt{3}) \) for the denominator.
Use the difference of squares formula: \((a + b)(a - b) = a^2 - b^2\). Apply this to the denominator: \((2)^2 - (\sqrt{3})^2 = 4 - 3 = 1\).
Simplify the expression: The denominator becomes 1, so the expression simplifies to \( (2 - \sqrt{3})^2 \). Expand and simplify the numerator to get the final expression.

 2:58m
2:58mWatch next
Master Rationalizing Denominators with a bite sized video explanation from Patrick
Start learning