Write a formula for the general or nth⁡n^{\th}nth term of the geometric sequence where a7=1458a_7=1458a7=1458 and r=−3r=-3r=−3.

a n = 2 ⋅ ( − 3 ) n − 1 a_{n}=2\cdot\left(-3\right)^{n-1} a n = 2 ⋅ ( − 3 ) n − 1

Write a formula for the general or n th ⁡ n^{\th} n t h term of the geometric sequence where a 7 = 1458 a_7=1458 a 7 = 1458 and r = − 3 r=-3 r = − 3 .

Everyone. So in this practice problem, we're gonna find a general formula or a formula for the general or nth term of a geometric sequence. And the information that we're given here says that a 7 is equal to a 1,458 and r is equal to negative 3. Let's go ahead and get started here. Remember the that the general form for a geometric sequence is a n equals a one times r to the n minus one power. So if I wanna figure out a general formula for this, I'm just gonna write that out. A n equals a one times r to the n minus 1. What I need from this equation in order in order to write it is I need to know what the first term is, and I need to know what the common ratio is. So let's do the inform let's look through the information that we're given, and we'll see that we actually have one of those variables already. We have r equals negative 3. So I have r. So can I just start writing this equation? Well, not quite. Because what we're told is that a 7 equals, 1458. We actually have no idea what the first term is. What is a 1? So in order to figure this out, what I'm gonna have to do over here is I'm gonna have to figure out what the first term of the sequence is. How do I do that? Well, let's just look at the information that I do know. I know that a 7 is equal to a 1,458. So what I can use here is I can use the fact that a 7, and I'm gonna just sort of use the general formula, is just equal to a one times r, in which case this is just gonna be negative 3, to the n minus one power, which is gonna be 6 in this case. Right? So here, I'm just looking I'm just using the fact that n is equal to 7. So this number right here, when I plug this in, even though I don't know what a one is equal to, I know that the 7th term is equal to a 1,458. So what I can use here is I can just use these, these numbers to actually figure out what a one is equal to. So go ahead and punch negative 3 to the 6th power into your calculators, and you'll see that this, simplifies down to a one times, and this is gonna be 729. Make sure when you plug it into your calculator that you're doing negative 3 in parentheses to the 6th power, because if you do it without the parentheses like this, you're you're gonna get a negative number. So be really careful when you do that. This is 729, and this is gonna be a 1,458. Now it's just pretty simple division. Right? So we're gonna divide 729 on each side, cancels out. And what you're gonna find here is that a one is equal to 2. So now that we know what the first term is, we can plug it back into our general formula. Alright? So we look for a general formula, just to recap. We actually used what one of the terms was. We know what the number is. We used the general formula to figure out what the first term is by using that equation, and now we can plug it in and find what the general formula is. Alright? So I'm just gonna plug this right back into this formula over here. And I have that a n is equal to 2 times negative three to the n minus one power. This is the general formula, and with this equation, I could figure out any term in the sequence, any nth term. Alright, folks. So that's it for this one. Let me know if you have any questions. Thanks for watching.

Write a formula for the general or n th ⁡ n^{\th} n t h term of the geometric sequence where a 7 = 1458 a_7=1458 a 7 = 1458 and r = − 3 r=-3 r = − 3 .

a n = 2 ⋅ ( − 3 ) n − 1 a_{n}=2\cdot\left(-3\right)^{n-1} a n = 2 ⋅ ( − 3 ) n − 1

a n = 1 ⋅ ( − 3 ) n − 1 a_{n}=1\cdot\left(-3\right)^{n-1} a n = 1 ⋅ ( − 3 ) n − 1

a n = − 2 3 ⋅ ( − 3 ) n − 1 a_{n}=-\frac23\cdot\left(-3\right)^{n-1} a n = − 3 2 ⋅ ( − 3 ) n − 1

a n = 2 3 ⋅ ( − 3 ) n − 1 a_{n}=\frac23\cdot\left(-3\right)^{n-1} a n = 3 2 ⋅ ( − 3 ) n − 1

20. Sequences, Series & Induction

Geometric Sequences

Precalculus

20. Sequences, Series & Induction

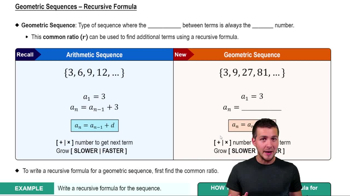
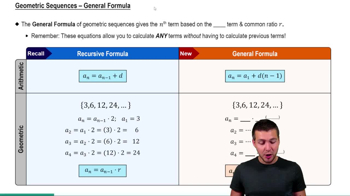
Geometric Sequences

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Write a formula for the general or $n^{\th}$ term of the geometric sequence where $a_7=1458$ and $r=-3$ .

$a_{n}=1\cdot\left(-3\right)^{n-1}$

$a_{n}=2\cdot\left(-3\right)^{n-1}$

$a_{n}=-\frac23\cdot\left(-3\right)^{n-1}$

$a_{n}=\frac23\cdot\left(-3\right)^{n-1}$

Verified step by step guidance

Identify the formula for the nth term of a geometric sequence, which is given by: <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mi>n</mi><mo>=</mo><mi>a</mi><mn>1</mn><mo>⋅</mo><msup><mi>r</mi><mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow></msup></math>, where <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mn>1</mn></math> is the first term and <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi></math> is the common ratio.

Use the given information that <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mn>7</mn><mo>=</mo><mn>1458</mn></math> and <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi><mo>=</mo><mo>-</mo><mn>3</mn></math> to set up the equation for the 7th term: <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>1458</mn><mo>=</mo><mi>a</mi><mn>1</mn><mo>⋅</mo><msup><mo>(</mo><mo>-</mo><mn>3</mn><mo>)</mo><mn>6</mn></msup></math>.

Calculate <math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mo>(</mo><mo>-</mo><mn>3</mn><mo>)</mo><mn>6</mn></msup></math> to find the value of the common ratio raised to the power of 6.

Solve for <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mn>1</mn></math> by dividing both sides of the equation by <math xmlns="http://www.w3.org/1998/Math/MathML"><msup><mo>(</mo><mo>-</mo><mn>3</mn><mo>)</mo><mn>6</mn></msup></math>.

Substitute the value of <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mn>1</mn></math> and <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>r</mi></math> into the nth term formula to write the general term: <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>a</mi><mi>n</mi><mo>=</mo><mi>a</mi><mn>1</mn><mo>⋅</mo><msup><mo>(</mo><mo>-</mo><mn>3</mn><mo>)</mo><mrow><mi>n</mi><mo>-</mo><mn>1</mn></mrow></msup></math>.

4:18m

Watch next

Master Geometric Sequences - Recursive Formula with a bite sized video explanation from Patrick

Start learning

Struggling with Precalculus?

Write a formula for the general or nth⁡n^{\th}nth term of the geometric sequence where a7=1458a_7=1458a7​=1458 and r=−3r=-3r=−3.

Watch next

Write a formula for the general or $n^{\th}$ term of the geometric sequence where $a_7=1458$ and $r=-3$ .