Using the graph, find the specified limit or state that the limit does not exist (DNE).lim⁡x→−2−f(x)\lim_{x\rarr-2^{-}}f\left(x\right)limx→−2−f(x), lim⁡x→−2+f(x)\lim_{x\rarr-2^{+}}f\left(x\right)limx→−2+f(x), lim⁡x→−2f(x)\lim_{x\rarr-2^{}}f\left(x\right)limx→−2f(x)

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 \lim_{x\rarr-2^{+}}f\left(x\right)=1 lim x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = 1 \lim_{x\rarr-2^{}}f\left(x\right)=1 lim x → − 2 f ( x ) = 1

Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → − 2 − f ( x ) \lim_{x\rarr-2^{-}}f\left(x\right) lim x → − 2 − f ( x ) , lim ⁡ x → − 2 + f ( x ) \lim_{x\rarr-2^{+}}f\left(x\right) lim x → − 2 + f ( x ) , lim ⁡ x → − 2 f ( x ) \lim_{x\rarr-2^{}}f\left(x\right) lim x → − 2 f ( x )

Using the graph, we wanna go ahead and find the specified limits or state that they don't exist. So let's go ahead and jump in here. Now the first limit that we're asked to find is a left sided limit, the limit of f of x as x approaches negative 2 from the left. So looking at our graph here, x approaching negative 2 coming in from this left side, I see that as x gets really, really close to negative 2 from the left, that my function is approaching a value of 1. So that's my limit there. Now looking next at my right sided limit, the limit of f of x as x approaches negative 2 from the right, Coming in now from that right side, approaching that value of negative 2, getting really, really close to it from the other side, I see again that my function is approaching a value of 1. Now since we found those one-sided limits, what's just our limit as x approaches a negative 2? Now since these limits are equal to each other, my left sided limit is equal to my right sided limit as x approaches negative 2. That tells me that my limit of f of x as x approaches negative 2 is simply equal to that same value 1. Now I'll see you in the next one. Thanks for watching.

Using the graph, find the specified limit or state that the limit does not exist (DNE). lim ⁡ x → − 2 − f ( x ) \lim_{x\rarr-2^{-}}f\left(x\right) lim x → − 2 − f ( x ) , lim ⁡ x → − 2 + f ( x ) \lim_{x\rarr-2^{+}}f\left(x\right) lim x → − 2 + f ( x ) , lim ⁡ x → − 2 f ( x ) \lim_{x\rarr-2^{}}f\left(x\right) lim x → − 2 f ( x )

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 \lim_{x\rarr-2^{+}}f\left(x\right)=1 lim x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = 1 \lim_{x\rarr-2^{}}f\left(x\right)=1 lim x → − 2 f ( x ) = 1

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = − 1 \lim_{x\rarr-2^{+}}f\left(x\right)=-1 lim x → − 2 + f ( x ) = − 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\rarr-2}f\left(x\right)=DNE lim x → − 2 f ( x ) = D NE

lim ⁡ x → − 2 − f ( x ) = 1 \lim_{x\rarr-2^{-}}f\left(x\right)=1 lim x → − 2 − f ( x ) = 1 , lim ⁡ x → − 2 + f ( x ) = 1 \lim_{x\rarr-2^{+}}f\left(x\right)=1 lim x → − 2 + f ( x ) = 1 , lim ⁡ x → − 2 f ( x ) = D N E \lim_{x\rarr-2}f\left(x\right)=DNE lim x → − 2 f ( x ) = D NE

lim ⁡ x → − 2 − f ( x ) = 0 \lim_{x\rarr-2^{-}}f\left(x\right)=0 lim x → − 2 − f ( x ) = 0 , lim ⁡ x → − 2 + f ( x ) = 0 \lim_{x\rarr-2^{+}}f\left(x\right)=0 lim x → − 2 + f ( x ) = 0 , lim ⁡ x → − 2 f ( x ) = 0 \lim_{x\rarr-2}f\left(x\right)=0 lim x → − 2 f ( x ) = 0

22. Limits & Continuity

Introduction to Limits

Precalculus

22. Limits & Continuity

Introduction to Limits

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

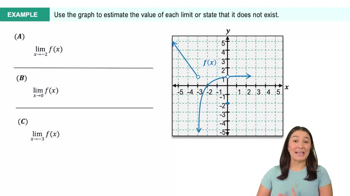
Using the graph, find the specified limit or state that the limit does not exist (DNE).
$\lim_{x\rarr-2^{-}}f\left(x\right)$ , $\lim_{x\rarr-2^{+}}f\left(x\right)$ , $\lim_{x\rarr-2^{}}f\left(x\right)$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{}}f\left(x\right)=1$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=-1$ , $\lim_{x\rarr-2}f\left(x\right)=DNE$

$\lim_{x\rarr-2^{-}}f\left(x\right)=1$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=1$ , $\lim_{x\rarr-2}f\left(x\right)=DNE$

$\lim_{x\rarr-2^{-}}f\left(x\right)=0$ , $\lim_{x\rarr-2^{+}}f\left(x\right)=0$ , $\lim_{x\rarr-2}f\left(x\right)=0$

Verified step by step guidance

To find the limit as x approaches -2 from the left, denoted as lim_{x \to -2^{-}} f(x), observe the graph as x approaches -2 from values less than -2. The graph approaches the y-value of 1.

To find the limit as x approaches -2 from the right, denoted as lim_{x \to -2^{+}} f(x), observe the graph as x approaches -2 from values greater than -2. The graph approaches the y-value of -1.

Since the left-hand limit (1) and the right-hand limit (-1) as x approaches -2 are not equal, the two-sided limit lim_{x \to -2} f(x) does not exist (DNE).

The limit from the left, lim_{x \to -2^{-}} f(x), is 1, and the limit from the right, lim_{x \to -2^{+}} f(x), is -1.

Therefore, the overall limit lim_{x \to -2} f(x) is DNE because the left-hand and right-hand limits are not equal.

6:47m

Watch next

Master Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick

Start learning