Without using a calculator, determine all values of P in the interval [ 0 ° , 90 ° ) \left[0\degree,90\degree\right) [ 0° , 90° ) with the following trigonometric function value. csc ⁡ P = 2 \csc P=\sqrt2 csc P = 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

Let's give this problem a try. So here we're told without using a calculator, determine all the values of p in the interval from 0 degrees to 90 degrees with the following trigonometric value. And we can see that we have the cosecant of p is equal to the square root of 2. So how can we go about solving this problem? Well, personally for me, there are a couple different ways that you could approach this. But I don't like seeing these cosecant values or secant values. I like to switch these to trigonometric values I'm a little bit more familiar with, like sine, cosine, and tangent. So what I'm gonna do is recognize with the reciprocal identities that cosecant of p is the same thing as one over the sine of p. And we can see that that's equal to the square root of 2. Now what I'm gonna do here is I'm going to multiply the sine of p on both sides of the equation. And this will allow me to cancel the sine of p on the left side, giving me that one is equal to the square root of 2 multiplied by the sine of p. From here, I'm going to divide the square root of 2 on both sides of this equation, and then I'll get the square root of 2's to cancel right there, giving me that the sine of p is equal to 1 over the square root of 2. Now from here before I do anything else, I'm actually not going to rationalize this denominator or do the inverse sign, because what I'm going to do instead is draw a right triangle. Now the reason that I'm drawing a right triangle is because this is going to show me what this function looks like and how the sides of this triangle relate, because recognize that I cannot use a calculator in this problem. So what we need to do is visually figure out what's going on here, or find some sort of method to solve for p. Now I recall from SOHCAHTOA that the sine of our angle is going to be opposite over hypotenuse when it comes to a right triangle. And so if I go ahead and see sin of p here, let's say that this is angle p in our right triangle. The sin of p is opposite over hypotenuse, so this would be the opposite side to our angle, which is 1. And then the hypotenuse is going to be the square root of 2, which is the long side of the triangle. Now from here, what I can do is solve for this missing leg. And to solve for this missing leg, I'm going to go ahead and say that this one right over here is a, this is b, and then the hypotenuse is always equal to c. So we can use the pythagorean theorem and say that a squared plus b squared is equal to c squared. A is 1, so we have 1 squared, plus b squared is equal to the square root of 2 squared. Now the square root and the square will cancel, meaning that we'll have one, because one squared is 1, plus b squared is equal to 2. Now from here, what I can do is I can take both sides of this equation and subtract 1. This will allow me to clear the ones on the left side giving me that b squared is equal to 2 minus 1, which is 1. And And then here I can take the square root on both sides of the equation, giving me that b is equal to just 1. So the missing side of this right triangle is 1. And notice the two legs are the same. Because these two legs match each other, that means these two angles must match each other. And if these two angles are the same and it's a right triangle, that means these two angles have to be 45 degrees each. So p has to be equal to 45 degrees, and we can tell just by observing that this is a 45, 45, 90 right triangle. So this is going to be our angle right here. That's the value for p and the solution to this problem. So hope you found this video helpful. Thanks for watching.

Without using a calculator, determine all values of P in the interval [ 0 ° , 90 ° ) \left[0\degree,90\degree\right) [ 0° , 90° ) with the following trigonometric function value. csc ⁡ P = 2 \csc P=\sqrt2 csc P = 2 <path d="M95,702 c-2.7,0,-7.17,-2.7,-13.5,-8c-5.8,-5.3,-9.5,-10,-9.5,-14 c0,-2,0.3,-3.3,1,-4c1.3,-2.7,23.83,-20.7,67.5,-54 c44.2,-33.3,65.8,-50.3,66.5,-51c1.3,-1.3,3,-2,5,-2c4.7,0,8.7,3.3,12,10 s173,378,173,378c0.7,0,35.3,-71,104,-213c68.7,-142,137.5,-285,206.5,-429 c69,-144,104.5,-217.7,106.5,-221 l0 -0 c5.3,-9.3,12,-14,20,-14 H400000v40H845.2724 s-225.272,467,-225.272,467s-235,486,-235,486c-2.7,4.7,-9,7,-19,7 c-6,0,-10,-1,-12,-3s-194,-422,-194,-422s-65,47,-65,47z M834 80h400000v40h-400000z">

P = 30 ° P=30\degree P = 30° only

P = 30 ° , 60 ° P=30°,60° P = 30° , 60°

8. Trigonometric Functions on Right Triangles

Special Right Triangles

Precalculus

8. Trigonometric Functions on Right Triangles

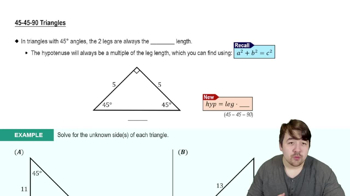
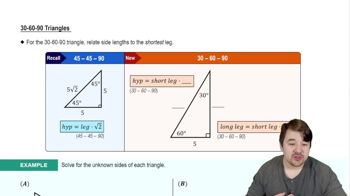
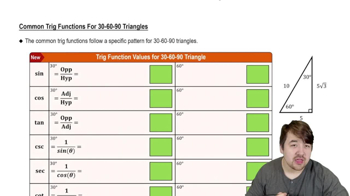
Special Right Triangles

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Without using a calculator, determine all values of P in the interval $\left[0\degree,90\degree\right)$ with the following trigonometric function value.
$\csc P=\sqrt2$

$P=30\degree$ only

$P=45°$ only

$P=60°$ only

$P=30°,60°$

Verified step by step guidance

Understand that the cosecant function, csc(P), is the reciprocal of the sine function, so csc(P) = 1/sin(P).

Given csc(P) = 2, rewrite this as 1/sin(P) = 2. This implies that sin(P) = 1/2.

Recall the unit circle and the special angles where the sine value is 1/2. These angles are typically 30° and 150°.

Since the problem restricts P to the interval [0°, 90°), we only consider angles within this range. Therefore, P = 30° is the only angle that satisfies sin(P) = 1/2 within the given interval.

Verify the solution by checking that csc(30°) = 1/sin(30°) = 2, confirming that P = 30° is correct within the specified interval.

4:34m

Watch next

Master 45-45-90 Triangles with a bite sized video explanation from Patrick

Start learning

Struggling with Precalculus?

Without using a calculator, determine all values of P in the interval [0°,90°)\left[0\degree,90\degree\right)[0°,90°) with the following trigonometric function value.csc⁡P=2\csc P=\sqrt2cscP=2​

Watch next

Without using a calculator, determine all values of P in the interval $\left[0\degree,90\degree\right)$ with the following trigonometric function value.
$\csc P=\sqrt2$