Skip to main content
Pearson+ LogoPearson+ Logo
Ch 22: Gauss' Law
All textbooksYoung & Freedman Calc 14th EditionCh 22: Gauss' LawProblem 29
Previous problem
Next problem
Chapter 22, Problem 29

An infinitely long cylindrical conductor has radius r and uniform surface charge density σ. (a) In terms of σ and R, what is the charge per unit length λ for the cylinder?

Verified step by step guidance
1
Identify the given quantities: the radius of the cylinder, r, and the uniform surface charge density, \( \sigma \).
Understand that the surface charge density, \( \sigma \), is defined as the charge per unit area on the surface of the cylinder.
To find the charge per unit length, \( \lambda \), consider a small segment of the cylinder of length L. The total charge, Q, on this segment can be calculated by multiplying the surface charge density by the surface area of the segment.
Calculate the surface area of the cylindrical segment, which is given by \( 2\pi r L \) where r is the radius and L is the length of the cylinder segment.
Express the charge per unit length, \( \lambda \), by dividing the total charge, Q, by the length of the cylinder segment, L. Simplify the expression to find \( \lambda \) in terms of \( \sigma \) and r.

Verified Solution

Video duration:
1m
This video solution was recommended by our tutors as helpful for the problem above.
Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Surface Charge Density (σ)

Surface charge density (σ) is defined as the amount of electric charge per unit area on a surface. It is typically measured in coulombs per square meter (C/m²). In the context of a cylindrical conductor, σ represents how much charge is distributed over the surface of the cylinder, which influences the electric field and potential around it.
Recommended video:
Guided course
04:03
Surface Charge Density

Charge per Unit Length (λ)

Charge per unit length (λ) refers to the total charge distributed along a length of a conductor, typically measured in coulombs per meter (C/m). For a cylindrical conductor, λ can be derived from the surface charge density by considering the surface area of the cylinder and the length over which the charge is distributed, allowing us to relate σ to λ.
Recommended video:
Guided course
10:54
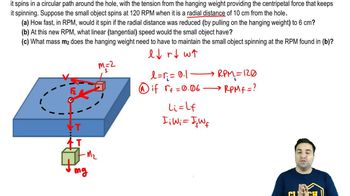
Spinning on a string of variable length

Gauss's Law

Gauss's Law states that the electric flux through a closed surface is proportional to the enclosed electric charge. This principle is crucial for analyzing the electric field around charged conductors. In the case of an infinitely long cylindrical conductor, Gauss's Law simplifies the calculation of the electric field and helps relate the surface charge density to the charge per unit length.
Recommended video:
Guided course
10:20
Gauss' Law
Previous problem
Next problem
Related Practice
Textbook Question
A conductor with an inner cavity, like that shown in Fig. 22.23c, carries a total charge of +5.00 nC. The charge within the cavity, insulated from the conductor, is −6.00 nC. How much charge is on (a) the inner surface of the conductor and (b) the outer surface of the conductor?
1445
views
Textbook Question
A very large, horizontal, nonconducting sheet of charge has uniform charge per unit area σ = 5.00×10−6 C/m2. (a) A small sphere of mass m = 8.00×10−6 kg and charge q is placed 3.00 cm above the sheet of charge and then released from rest. (a) If the sphere is to remain motionless when it is released, what must be the value of q?
1036
views
Textbook Question
A very large, horizontal, nonconducting sheet of charge has uniform charge per unit area σ = 5.00×10−6 C/m2. (a) A small sphere of mass m = 8.00×10−6 kg and charge q is placed 3.00 cm above the sheet of charge and then released from rest. (b) What is q if the sphere is released 1.50 cm above the sheet?
385
views
Textbook Question
An infinitely long cylindrical conductor has radius r and uniform surface charge density σ. (b) In terms of σ, what is the magnitude of the electric field produced by the charged cylinder at a distance r > R from its axis? (c) Express the result of part (b) in terms of λ and show that the electric field outside the cylinder is the same as if all the charge were on the axis.
2739
views
1
rank
Textbook Question
A very long conducting tube (hollow cylinder) has inner radius A and outer radius b. It carries charge per unit length +α, where α is a positive constant with units of C/m. A line of charge lies along the axis of the tube. The line of charge has charge per unit length +α. (b) What is the charge per unit length on (i) the inner surface of the tube and (ii) the outer surface of the tube?
1925
views
Textbook Question
A very long conducting tube (hollow cylinder) has inner radius A and outer radius b. It carries charge per unit length +α, where α is a positive constant with units of C/m. A line of charge lies along the axis of the tube. The line of charge has charge per unit length +α. (a) Calculate the electric field in terms of α and the distance r from the axis of the tube for (i) r < a; (ii) a < r < b; (iii) r > b. Show your results in a graph of E as a function of R.
889
views
1
rank