A planet orbiting a distant star has radius 3.24 * 10^6 m. The escape speed for an object launched from this planet’s surface is 7.65 * 10^3 m/s. What is the acceleration due to gravity at the surface of the planet?
Ch 13: Gravitation
Chapter 13, Problem 13.35
Consider the ringshaped body of Fig. E13.35<IMAGE>. A particle with mass m is placed a distance x from the center of the ring, along the line through the center of the ring and perpendicular to its plane. (a) Calculate the gravitational potential energy U of this system. Take the potential energy to be zero when the two objects are far apart. (b) Show that your answer to part (a) reduces to the expected result when x is much larger than the radius a of the ring. (c) Use Fx = -dU>dx to find the magnitude and direction of the force on the particle (see Section 7.4). (d) Show that your answer to part (c) reduces to the expected result when x is much larger than a. (e) What are the values of U and Fx when x = 0? Explain why these results make sense.
 Verified step by step guidance
Verified step by step guidance1
Step 1: To calculate the gravitational potential energy U of the system, consider the mass distribution of the ring and the mass m at a distance x from the center. Use the formula for gravitational potential energy due to a point mass, U = -GmM/r, where G is the gravitational constant, M is the mass of the ring, and r is the distance between the mass m and a differential mass element dm on the ring.
Step 2: Integrate the expression for U over the entire ring, taking into account the geometry of the problem. The distance r from any point on the ring to the mass m can be expressed using the Pythagorean theorem as r = \sqrt{x^2 + a^2}, where a is the radius of the ring.
Step 3: For part (b), simplify the expression for U when x is much larger than a (x >> a). In this limit, r approximately equals x, and the expression for U should simplify to the potential energy of two point masses separated by distance x.
Step 4: To find the force Fx on the particle, use the relation Fx = -dU/dx. Calculate the derivative of U with respect to x, considering the integral expression derived in Step 2.
Step 5: For part (d), analyze the behavior of Fx when x is much larger than a, and for part (e), evaluate U and Fx when x = 0. Discuss why these results are physically reasonable, considering the symmetry and distribution of mass in the ring.

Verified Solution
Video duration:
8mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Gravitational Potential Energy
Gravitational potential energy (U) is the energy an object possesses due to its position in a gravitational field. It is defined relative to a reference point, typically where the potential energy is considered zero, such as when objects are infinitely far apart. For a mass m at a distance x from a mass distribution, U can be calculated by integrating the gravitational force over the distance. Understanding this concept is crucial for solving problems involving gravitational interactions.
Recommended video:
Guided course

Gravitational Potential Energy
Force and Potential Energy Relationship
The relationship between force (F) and potential energy (U) is given by the equation F = -dU/dx, which indicates that the force acting on an object is the negative gradient of the potential energy with respect to position. This means that the force points in the direction of decreasing potential energy. This concept is essential for determining the force acting on the particle in the given problem, as it allows us to derive the force from the potential energy function.
Recommended video:
Guided course
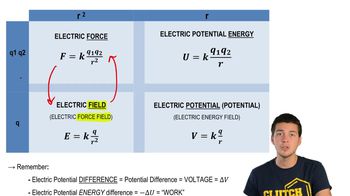
Relationships Between Force, Field, Energy, Potential
Limitations and Approximations in Physics
In physics, approximations are often used to simplify complex problems. In this context, when the distance x is much larger than the radius a of the ring, the gravitational effects can be approximated as if the mass were concentrated at a point. This simplification allows for easier calculations and helps verify that the derived expressions for potential energy and force align with expected results in classical mechanics, reinforcing the validity of the models used.
Recommended video:
Guided course

Derivatives & Integrals
Related Practice
Textbook Question
137
views
Textbook Question
A uniform, solid, 1000.0-kg sphere has a radius of 5.00 m. (a) Find the gravitational force this sphere exerts on a 2.00-kg point mass placed at the following distances from the center of the sphere: (i) 5.01 m, (ii) 2.50 m.
146
views
Textbook Question
A thin, uniform rod has length L and mass M. A small uniform sphere of mass m is placed a distance x from one end of the rod, along the axis of the rod (Fig. E13.34)<IMAGE>. (a) Calculate the gravitational potential energy of the rod–sphere system. Take the potential energy to be zero when the rod and sphere are infinitely far apart. Show that your answer reduces to the expected result when x is much larger than L.
142
views
