A 6.0-kg box moving at 3.0 m/s on a horizontal, frictionless surface runs into a light spring of force constant 75 N/cm. Use the work–energy theorem to find the maximum compression of the spring.

Verified step by step guidance

1. Identify the initial kinetic energy of the box using the formula for kinetic energy, KE = \(\frac{1}{2}mv^2\), where \(m\) is the mass of the box and \(v\) is its velocity.
2. Understand that the box will compress the spring until all its kinetic energy is converted into potential energy stored in the spring. The potential energy stored in a compressed spring is given by \(PE = \frac{1}{2}kx^2\), where \(k\) is the spring constant and \(x\) is the compression of the spring.
3. Set the kinetic energy equal to the potential energy to create an equation: \(\frac{1}{2}mv^2 = \frac{1}{2}kx^2\).
4. Solve for \(x\) by isolating \(x\) on one side of the equation. This involves dividing both sides by \(\frac{1}{2}k\) and then taking the square root of both sides.
5. Convert the spring constant from N/cm to N/m by multiplying by 100, as the units need to be consistent for the calculations.

Key Concepts

Work-Energy Theorem

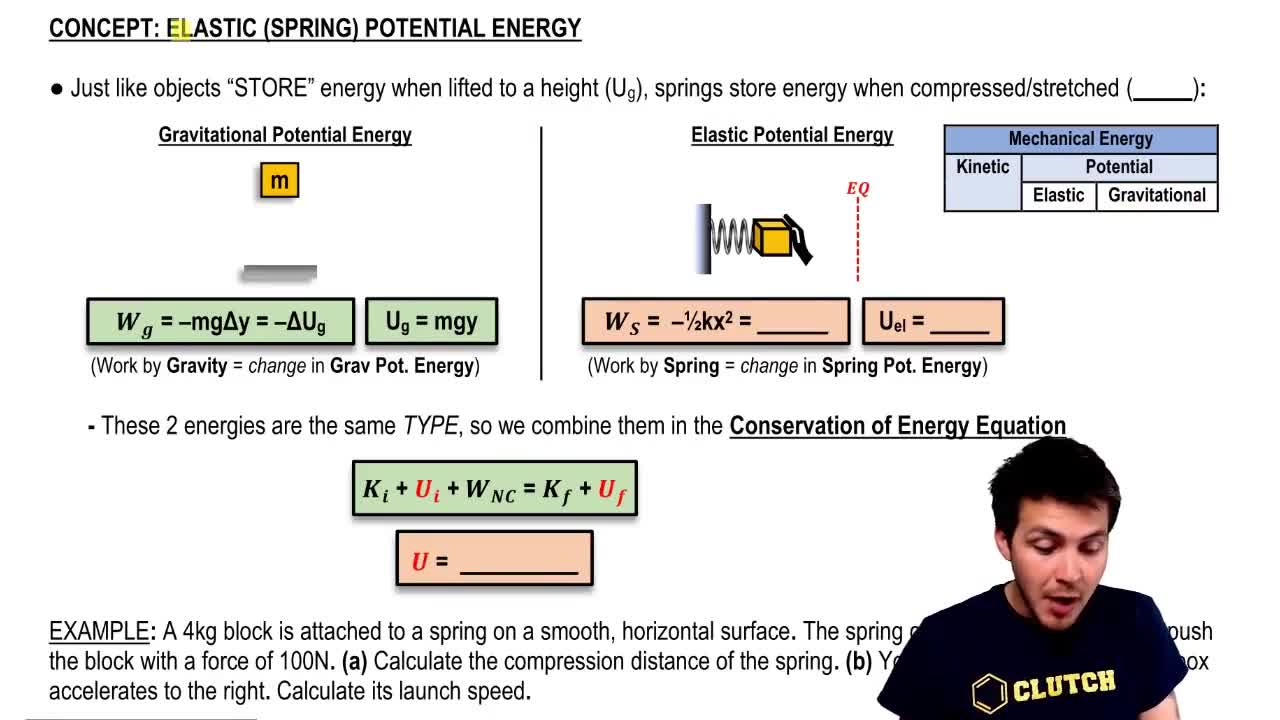
The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. In this scenario, the kinetic energy of the box will be converted into the potential energy stored in the spring as it compresses. This principle allows us to relate the initial kinetic energy of the box to the maximum potential energy of the spring at maximum compression.

Kinetic Energy

Kinetic energy is the energy an object possesses due to its motion, calculated using the formula KE = 1/2 mv², where m is the mass and v is the velocity. For the box in this problem, its initial kinetic energy can be determined using its mass (6.0 kg) and its velocity (3.0 m/s). This energy will be transferred to the spring as it compresses.

Spring Potential Energy

Spring potential energy is the energy stored in a compressed or stretched spring, given by the formula PE = 1/2 kx², where k is the spring constant and x is the compression or extension from its equilibrium position. In this case, the spring constant is given as 75 N/cm, which must be converted to N/m for calculations. The maximum compression of the spring can be found by equating the initial kinetic energy of the box to the potential energy of the spring.