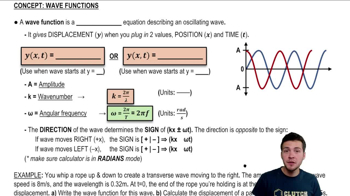
Here are the essential concepts you must grasp in order to answer the question correctly.
Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and is subject to gravitational forces. It can be analyzed by breaking it into horizontal and vertical components. The angle of launch, initial speed, and height reached are critical factors in determining the trajectory and range of the projectile.
Recommended video:
Introduction to Projectile Motion
Kinematic Equations
Kinematic equations describe the motion of objects under constant acceleration, such as gravity. These equations relate displacement, initial velocity, final velocity, acceleration, and time. For vertical motion, the equation that connects maximum height with initial velocity and launch angle is particularly useful in solving for takeoff speed.
Recommended video:
Trigonometric Functions
Trigonometric functions, such as sine and cosine, are essential for resolving the components of the initial velocity in projectile motion. When an object is launched at an angle, the initial velocity can be split into horizontal and vertical components using these functions. This allows for the calculation of the vertical component needed to reach a specific height.
Recommended video:
 Verified step by step guidance
Verified step by step guidance