Ch 29: The Magnetic Field
Chapter 26, Problem 29.64
FIGURE P29.64 shows a mass spectrometer, an analytical instrument used to identify the various molecules in a sample by measuring their charge-to-mass ratio q/m. The sample is ionized, the positive ions are accelerated (starting from rest) through a potential difference ∆V, and they then enter a region of uniform magnetic field. The field bends the ions into circular trajectories, but after just half a circle they either strike the wall or pass through a small opening to a detector. As the accelerating voltage is slowly increased, different ions reach the detector and are measured. Consider a mass spectrometer with a 200.00 mT magnetic field and an 8.0000 cm spacing between the entrance and exit holes. To five significant figures, what accelerating potential differences ∆V are required to detect the ions (a) O₂⁺ (b) N₂⁺ and (c) CO⁺? See Exercise 29 for atomic masses; the mass of the missing electron is less than 0.001 u and is not relevant at this level of precision. Although N₂⁺ and CO⁺ both have a nominal molecular mass of 28, they are easily distinguished by virtue of their slightly different accelerating voltages. Use the following constants: 1 u = 1.6605 x 10⁻²⁷ kg, e = 1.6022 x 10⁻¹⁹ C. <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Calculate the radius of the circular path for the ions in the magnetic field. Use the formula for the radius \( r = \frac{mv}{qB} \), where \( m \) is the mass of the ion, \( v \) is the velocity of the ion, \( q \) is the charge of the ion, and \( B \) is the magnetic field strength.
Determine the velocity \( v \) of the ions using the kinetic energy gained from the accelerating potential difference, \( \Delta V \). The kinetic energy imparted to the ions is given by \( q \Delta V \), and since the ions start from rest, their kinetic energy is also \( \frac{1}{2} mv^2 \). Equate these to find \( v = \sqrt{\frac{2q \Delta V}{m}} \).
Substitute the expression for \( v \) from step 2 into the radius equation from step 1. This gives \( r = \frac{m \sqrt{\frac{2q \Delta V}{m}}}{qB} = \sqrt{\frac{2m \Delta V}{qB^2}} \).
Solve for \( \Delta V \) using the radius \( r \) that corresponds to the distance the ions travel before reaching the detector. Since the ions travel half a circle, the diameter of the circle (which is twice the radius) equals the spacing between the entrance and exit holes. Thus, \( 2r = 8.0000 \text{ cm} \). Rearrange the equation from step 3 to find \( \Delta V = \frac{(2r)^2 qB^2}{8m} \).
Calculate \( \Delta V \) for each ion (O₂⁺, N₂⁺, and CO⁺) using their respective masses and the charge \( q = e \), where \( e \) is the elementary charge. Use the given values for \( B \), \( e \), and the atomic mass unit conversion to find the mass in kilograms for each ion.

Verified Solution
Video duration:
7mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Charge-to-Mass Ratio (q/m)
The charge-to-mass ratio (q/m) is a fundamental property of ions that describes how much charge an ion carries relative to its mass. In mass spectrometry, this ratio is crucial because it determines how ions will behave in electric and magnetic fields. Ions with different q/m values will follow different trajectories, allowing for their separation and identification based on their unique paths.
Recommended video:
Guided course

Find Mass-to-Charge Ratio in Spectrometer
Acceleration through Potential Difference (∆V)
When ions are accelerated through a potential difference (∆V), they gain kinetic energy proportional to the charge of the ion and the voltage applied. This energy is given by the equation KE = q∆V, where KE is the kinetic energy. The resulting speed of the ions affects their trajectory in the magnetic field, influencing their detection in the mass spectrometer.
Recommended video:
Guided course

Potential Difference Between Two Charges
Magnetic Field and Circular Motion
In a magnetic field, charged particles experience a force that causes them to move in circular paths. The radius of this circular motion is determined by the ion's velocity, charge, mass, and the strength of the magnetic field. The relationship between these variables is described by the Lorentz force, which is essential for understanding how ions are deflected and detected in a mass spectrometer.
Recommended video:
Guided course
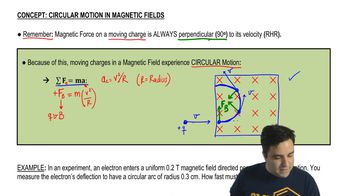
Circular Motion of Charges in Magnetic Fields
0
