The gasoline engine in your car can be modeled as the Otto cycle shown in FIGURE CP21.73. A fuel-air mixture is sprayed into the cylinder at point 1, where the piston is at its farthest distance from the spark plug. This mixture is compressed as the piston moves toward the spark plug during the adiabatic compression stroke. The spark plug fires at point 2, releasing heat energy that had been stored in the gasoline. The fuel burns so quickly that the piston doesn't have time to move, so the heating is an isochoric process. The hot, high-pressure gas then pushes the piston outward during the power stroke. Finally, an exhaust value opens to allow the gas temperature and pressure to drop back to their initial values before starting the cycle over again. a. Analyze the Otto cycle and show that the work done per cycle is

Verified step by step guidance

1. Identify the four main processes in the Otto cycle: (1) adiabatic compression, (2) isochoric heating, (3) adiabatic expansion, and (4) isochoric cooling.
2. Apply the first law of thermodynamics to each process. For adiabatic processes, the change in internal energy equals the work done (\(\Delta U = W\)), and for isochoric processes, the change in internal energy equals the heat added (\(\Delta U = Q\)).
3. Calculate the work done during the adiabatic compression and expansion. Remember that work done by the system is positive, so it will be positive during expansion and negative during compression.
4. Determine the net work done over the entire cycle by adding the work done during each process. The work done during isochoric processes is zero because the volume does not change.
5. Understand that the efficiency of the cycle can also be analyzed by comparing the work output to the heat input during the isochoric heating process.

Key Concepts

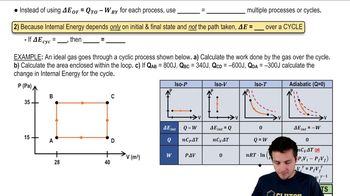
Otto Cycle

The Otto cycle is a thermodynamic cycle that describes the functioning of a gasoline engine. It consists of four main processes: adiabatic compression, isochoric heat addition, adiabatic expansion, and isochoric heat rejection. Understanding this cycle is crucial for analyzing the efficiency and work output of the engine, as it illustrates how energy is converted from fuel into mechanical work.

Adiabatic Process

An adiabatic process is one in which no heat is exchanged with the surroundings. In the context of the Otto cycle, both the compression and expansion strokes are adiabatic, meaning that the temperature and pressure of the gas change without heat transfer. This concept is essential for calculating the work done during these strokes, as it influences the internal energy of the gas.

Isochoric Process

An isochoric process occurs at constant volume, meaning that the gas does not expand or contract during the process. In the Otto cycle, the combustion of the fuel-air mixture happens during an isochoric process, where heat is added to the gas without changing its volume. This concept is important for understanding how the pressure and temperature of the gas increase rapidly, leading to the subsequent power stroke.