Here are the essential concepts you must grasp in order to answer the question correctly.
Root Mean Square Speed (rms speed)
The root mean square speed is a measure of the average speed of particles in a gas, calculated as the square root of the average of the squares of the speeds of individual molecules. It is directly related to the temperature and mass of the gas, providing insight into the kinetic energy of the molecules. For an ideal gas, the rms speed can be expressed using the formula v_rms = sqrt(3kT/m), where k is the Boltzmann constant, T is the temperature in Kelvin, and m is the mass of a molecule.
Recommended video:
Root-Mean-Square Speed of Ideal Gases
First Law of Thermodynamics
The First Law of Thermodynamics states that energy cannot be created or destroyed, only transformed from one form to another. In the context of gas compression, this principle implies that the work done on the gas and the heat transferred can change the internal energy of the gas. Mathematically, it can be expressed as ΔU = Q - W, where ΔU is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
Recommended video:
The First Law of Thermodynamics
Kinetic Energy and Temperature Relationship
The kinetic energy of gas molecules is directly related to the temperature of the gas. As the temperature increases, the average kinetic energy of the molecules also increases, which in turn affects their speeds. The relationship can be expressed as KE = (3/2)kT for a monatomic ideal gas, where KE is the average kinetic energy per molecule, k is the Boltzmann constant, and T is the absolute temperature. Changes in internal energy due to work and heat transfer will thus influence the rms speed of the gas molecules.
Recommended video:
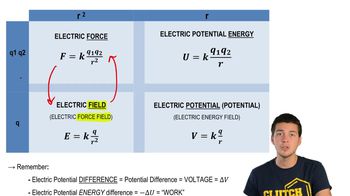
Relationships Between Force, Field, Energy, Potential
 Verified step by step guidance
Verified step by step guidance